题目内容
设集合M={(x,y)|x2+y2≤4},N={(x,y)|(x-1)2+(y-1)2≤r2(r>0)},当M∩N=N时,则实数r的取值范围为 .
【答案】分析:由已知中集合N={(x,y)|(x-1)2+(y-1)2≤r2,r>0},M={(x,y)|x2+y2≤4},若M∩N=N,判断出两个集合中的圆关系为内切或内含,由圆心距与半径之间的关系,构造关于r的不等式,解不等式即可得到实数r的取值范围.
解答:解:若M∩N=N,则N与M表示的圆内切或内含
由于N中的圆的圆心为N(1,1),半径为r,
M中的圆的圆心为M(0,0),半径为2,
则2-r≥|MN|=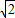 ,
,
∴0<r≤2-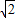 ,
,
故答案为:(0,2-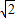 ].
].
点评:本题考查的知识点是圆与圆的位置关系及其判定,其中根据集合之间的关系,转化为圆与圆的位置关系,进而转化为圆心距与半径差之间的关系,是解答本题的关键.
解答:解:若M∩N=N,则N与M表示的圆内切或内含
由于N中的圆的圆心为N(1,1),半径为r,
M中的圆的圆心为M(0,0),半径为2,
则2-r≥|MN|=
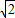 ,
,∴0<r≤2-
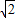 ,
,故答案为:(0,2-
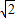 ].
].点评:本题考查的知识点是圆与圆的位置关系及其判定,其中根据集合之间的关系,转化为圆与圆的位置关系,进而转化为圆心距与半径差之间的关系,是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,B={(x,y)|2m≤x+y≤2m+1,x,y∈R},若A∩B≠∅,则实数m的取值范围是 .
,B={(x,y)|2m≤x+y≤2m+1,x,y∈R},若A∩B≠∅,则实数m的取值范围是 . ,B={(x,y)|2m≤x+y≤2m+1,x,y∈R},若A∩B≠∅,则实数m的取值范围是 .
,B={(x,y)|2m≤x+y≤2m+1,x,y∈R},若A∩B≠∅,则实数m的取值范围是 . ,B={(x,y)|2m≤x+y≤2m+1,x,y∈R},若A∩B≠∅,则实数m的取值范围是 .
,B={(x,y)|2m≤x+y≤2m+1,x,y∈R},若A∩B≠∅,则实数m的取值范围是 .