题目内容
设直线2x-y+1=0与椭圆
+
=1相交于A、B两点.
(1)线段AB中点M的坐标及线段AB的长;
(2)已知椭圆具有性质:设A、B是椭圆
+
=1上的任意两点,M是线段AB的中点,若直线AB、OM的斜率都存在,并记为kAB,kOM,则kAB?kOM为定值.试对双曲线
-
=1写出具有类似特性的性质,并加以证明.
| x2 |
| 3 |
| y2 |
| 4 |
(1)线段AB中点M的坐标及线段AB的长;
(2)已知椭圆具有性质:设A、B是椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
(1)设A(x1,y1)、B(x2,y2),则
?
x2+x-
=0?
(2分)
所以M(-
,
)
|AB|=
| x1-x2|=
=
(2)设A、B是双曲线
-
=1上的任意两点,M是线段AB的中点,若直线AB、OM的斜率都存在,并记为kAB,kOM,则kAB?kOM为定值.
证明:设A(x1,y1)、B(x2,y2),分别代入双曲线
-
=1,再相减后可得:
(x1+x2)(x1-x2)-
(y1+y2)(y1-y2)=0
设M(x0,y0),则
,代入上式可得
=
×
即kAB?kOM=
∴定值为
|
| 4 |
| 3 |
| 3 |
| 4 |
|
所以M(-
| 3 |
| 8 |
| 1 |
| 4 |
|AB|=
| 1+22 |
| 5 |
| (x1+x2)2-4x1x2 |
| 15 |
| 4 |
(2)设A、B是双曲线
| x2 |
| a2 |
| y2 |
| b2 |
证明:设A(x1,y1)、B(x2,y2),分别代入双曲线
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| a2 |
| 1 |
| b2 |
设M(x0,y0),则
|
| y1-y2 |
| x1-x2 |
| b2 |
| a2 |
| x0 |
| y0 |
即kAB?kOM=
| b2 |
| a2 |
∴定值为
| b2 |
| a2 |

练习册系列答案
相关题目
 ,
,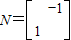 .在平面直角坐标系中,设直线2x-y+1=0在矩阵MN对应的变换作用下得到曲线F,求曲线F的方程.
.在平面直角坐标系中,设直线2x-y+1=0在矩阵MN对应的变换作用下得到曲线F,求曲线F的方程.