题目内容
(本小题满分16分)已知函数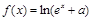 (
( 为常数)是实数集
为常数)是实数集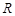 上的奇函数,函数
上的奇函数,函数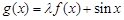 是区间
是区间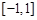 上的减函数。
上的减函数。
(1)求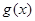 在
在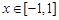 上的最大值;
上的最大值;
(2)若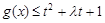 对
对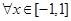 及
及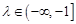 恒成立,求
恒成立,求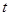 的取值范围;
的取值范围;
(3)讨论关于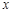 的方程
的方程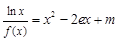 的根的个数。
的根的个数。
(1)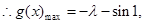 (2)
(2)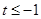
(3)①当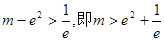 时,方程无解.
时,方程无解.
②当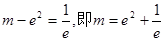 时,方程有一个根.
时,方程有一个根.
③当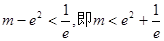 时,方程有两个根.
时,方程有两个根.
解析试题分析:(1)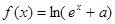 是奇函数,
是奇函数,
则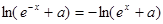 恒成立.
恒成立.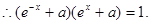
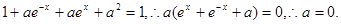
又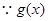 在[-1,1]上单调递减,
在[-1,1]上单调递减,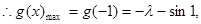 ……5分
……5分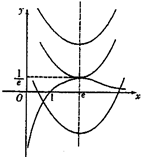
(2)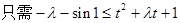 在
在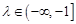 上恒成立,
上恒成立,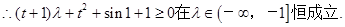
令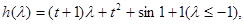 则
则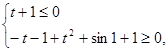
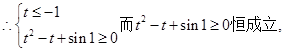
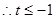 . ……10分
. ……10分
(3)由(1)知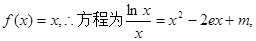
令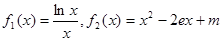 ,
,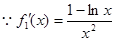 ,
,
当 上为增函数;
上为增函数; 上为减函数,
上为减函数,
当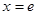 时,
时,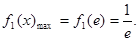
而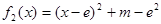 ,
,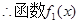 、
、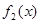 在同一坐标系的大致图象如图所示,
在同一坐标系的大致图象如图所示,
∴①当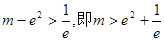 时,方程无解.
时,方程无解.
②当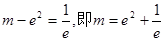 时,方程有一个根.
时,方程有一个根.
③当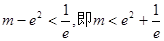 时,方程有两个根. ……16分
时,方程有两个根. ……16分
考点:本小题主要考查函数的性质和导数的应用.
点评:导数是研究函数的单调性、极值、最值的有力工具,经常考查,而且函数的其它性质如奇偶性、周期性、对称性等也经常综合考查,要综合运用所学知识解决问题,思维要严密,分类讨论时要尽量做到不重不漏.

练习册系列答案
相关题目
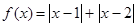 .
.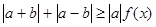 ,(a¹0,a、bÎR)恒成立,求实数x的范围.
,(a¹0,a、bÎR)恒成立,求实数x的范围.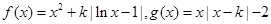 ,其中
,其中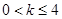 .(1) 讨论函数
.(1) 讨论函数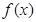 的单调性,并求出
的单调性,并求出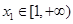 ,都存在
,都存在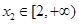 ,使得
,使得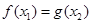 ,求实数
,求实数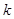 的取值范围.
的取值范围.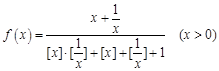 ,其中
,其中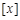 表示不超过
表示不超过 的最大整数,如
的最大整数,如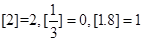 .
.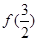 的值;
的值;  上存在x,使得
上存在x,使得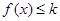 成立,求实数k的取值范围;
成立,求实数k的取值范围; 的值域.
的值域. 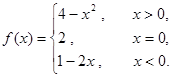
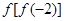 的值;
的值;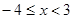 时,求函数
时,求函数 的值域。
的值域。
 上是增函数还是减函数?并用定义证明.
上是增函数还是减函数?并用定义证明.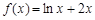 ,
,
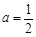 ,求
,求 的单调区间;
的单调区间; 时,求证:
时,求证: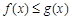 .
.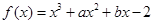 的图象过点
的图象过点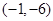 ,且函数
,且函数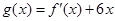 的图象关于
的图象关于 轴对称;
轴对称;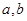 的值及函数
的值及函数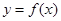 的单调区间;
的单调区间; 是定义在R上的奇函数,且对任意
是定义在R上的奇函数,且对任意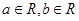 ,当
,当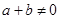 时,都有
时,都有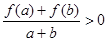 .
.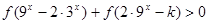 对任意
对任意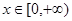 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.