题目内容
已知数集A={a1，a2，…，an}（1=a1＜a2＜…＜an，n≥2）具有性质P：对任意的k（2≤k≤n），?i，j（1≤i≤j≤n），使得ak=ai+aj成立．（Ⅰ）分别判断数集{1，3，4}与{1，2，3，6}是否具有性质P，并说明理由；
（Ⅱ）求证：an≤2a1+a2+…+an-1（n≥2）；
（Ⅲ）若an=72，求数集A中所有元素的和的最小值．
【答案】分析：（Ⅰ）利用性质P的概念，对数集{1，3，4}与{1，2，3，6}判断即可；
（Ⅱ）利用集合A={a1，a2，…，an}具有性质P，可分析得到ai≤ak-1，aj≤ak-1，从而ak=ai+aj≤2ak-1，（k=2，3，…n），将上述不等式相加得a2+…+an-1+an≤2（a1+a2+…+an-1）
即可证得结论；
（Ⅲ）首先注意到a1=1，根据性质P，得到a2=2a1=2，构造A={1，2，3，6，9，18，36，72}或者A={1，2，4，5，9，18，36，72}，这两个集合具有性质P，此时元素和为147．
再利用反证法证明满足S=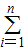
ai≤147最小的情况不存在，从而可得最小值为147．
解答：解：（Ⅰ）因为 3≠1+1，所以{1，3，4}不具有性质P．
因为 2=1×2，3=1+2，6=3+3，所以{1，2，3，6}具有性质P …（4分）
（Ⅱ）因为集合A={a1，a2，…，an}具有性质P：
即对任意的k（2≤k≤n），?i，j（1≤i≤j≤n），使得ak=ai+aj成立，
又因为1=a1＜a2＜…＜an，n≥2，所以ai＜ak，aj＜ak
所以ai≤ak-1，aj≤ak-1，所以ak=ai+aj≤2ak-1
即an-1≤2an-2，an-2≤2an-3，…，a3≤2a2，a2≤2a1…（6分）
将上述不等式相加得a2+…+an-1+an≤2（a1+a2+…+an-1）
所以an≤2a1+a2+…+an-1…（9分）
（Ⅲ）最小值为147．
首先注意到a1=1，根据性质P，得到a2=2a1=2
所以易知数集A的元素都是整数．
构造A={1，2，3，6，9，18，36，72}或者A={1，2，4，5，9，18，36，72}，这两个集合具有性质P，此时元素和为147．
下面，我们证明147是最小的和
假设数集A={a1，a2，…，an}（a1＜a2＜…＜an，n≥2），满足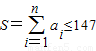
最小（存在性显然，因为满足
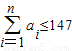的数集A只有有限个）．
第一步：首先说明集合A={a1，a2，…，an}（a1＜a2＜…＜an，n≥2）中至少有8个元素：
由（Ⅱ）可知a2≤2a1，a3≤2a2…
又a1=1，所以a2≤2，a3≤4，a4≤8，a5≤16，a6≤32，a7≤64＜72，
所以n≥8
第二步：证明an-1=36，an-2=18，an-3=9：
若36∈A，设at=36，因为an=72=36+36，为了使得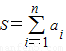
最小，在集合A
中一定不含有元素ak，使得36＜ak＜72，从而an-1=36；
假设36∉A，根据性质P，对an=72，有ai，aj，使得an=72=ai+aj
显然ai≠aj，所以an+ai+aj=144
而此时集合A中至少还有5个不同于an，ai，aj的元素，
从而S＞（an+ai+aj）+5a1=149，矛盾，
所以36∈A，进而at=36，且an-1=36；
同理可证：an-2=18，an-3=9
（同理可以证明：若18∈A，则an-2=18）．
假设18∉A．
因为an-1=36，根据性质P，有ai，aj，使得an-1=36=ai+aj
显然ai≠aj，所以an+an-1+ai+aj=144，
而此时集合A中至少还有4个不同于an，an-1，ai，aj的元素
从而S＞an+an-1+ai+aj+4a1=148，矛盾，
所以18∈A，且an-2=18
同理可以证明：若9∈A，则an-3=9
假设9∉A
因为an-2=18，根据性质P，有ai，aj，使得an-2=18=ai+aj
显然ai≠aj，所以an+an-1+an-2+ai+aj=144
而此时集合A中至少还有3个不同于an，an-1，an-2，ai，aj的元素
从而S＞an+an-1+an-2+ai+aj+3a1=147，矛盾，
所以9∈A，且an-3=9）
至此，我们得到了an-1=36，an-2=18，an-3=9ai=7，aj=2．
根据性质P，有ai，aj，使得9=ai+aj
我们需要考虑如下几种情形：
①ai=8，aj=1，此时集合中至少还需要一个大于等于4的元素ak，才能得到元素8，
则S＞148；
②，此时集合中至少还需要一个大于4的元素ak，才能得到元素7，
则S＞148；
③ai=6，aj=3，此时集合A={1，2，3，6，9，18，36，72}的和最小，为147；
④ai=5，aj=4，此时集合A={1，2，4，5，9，18，36，72}的和最小，为147．…（14分）
点评：本题考查数列的求和，突出考查反证法的应用，考查分类讨论思想与转化思想，考查构造函数的思想，an-1=36，an-2=18的证明是难点，属于难题．
（Ⅱ）利用集合A={a1，a2，…，an}具有性质P，可分析得到ai≤ak-1，aj≤ak-1，从而ak=ai+aj≤2ak-1，（k=2，3，…n），将上述不等式相加得a2+…+an-1+an≤2（a1+a2+…+an-1）
即可证得结论；
（Ⅲ）首先注意到a1=1，根据性质P，得到a2=2a1=2，构造A={1，2，3，6，9，18，36，72}或者A={1，2，4，5，9，18，36，72}，这两个集合具有性质P，此时元素和为147．
再利用反证法证明满足S=
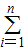ai≤147最小的情况不存在，从而可得最小值为147．解答：解：（Ⅰ）因为 3≠1+1，所以{1，3，4}不具有性质P．
因为 2=1×2，3=1+2，6=3+3，所以{1，2，3，6}具有性质P …（4分）
（Ⅱ）因为集合A={a1，a2，…，an}具有性质P：
即对任意的k（2≤k≤n），?i，j（1≤i≤j≤n），使得ak=ai+aj成立，
又因为1=a1＜a2＜…＜an，n≥2，所以ai＜ak，aj＜ak
所以ai≤ak-1，aj≤ak-1，所以ak=ai+aj≤2ak-1
即an-1≤2an-2，an-2≤2an-3，…，a3≤2a2，a2≤2a1…（6分）
将上述不等式相加得a2+…+an-1+an≤2（a1+a2+…+an-1）
所以an≤2a1+a2+…+an-1…（9分）
（Ⅲ）最小值为147．
首先注意到a1=1，根据性质P，得到a2=2a1=2
所以易知数集A的元素都是整数．
构造A={1，2，3，6，9，18，36，72}或者A={1，2，4，5，9，18，36，72}，这两个集合具有性质P，此时元素和为147．
下面，我们证明147是最小的和
假设数集A={a1，a2，…，an}（a1＜a2＜…＜an，n≥2），满足
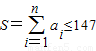最小（存在性显然，因为满足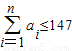的数集A只有有限个）．第一步：首先说明集合A={a1，a2，…，an}（a1＜a2＜…＜an，n≥2）中至少有8个元素：
由（Ⅱ）可知a2≤2a1，a3≤2a2…
又a1=1，所以a2≤2，a3≤4，a4≤8，a5≤16，a6≤32，a7≤64＜72，
所以n≥8
第二步：证明an-1=36，an-2=18，an-3=9：
若36∈A，设at=36，因为an=72=36+36，为了使得
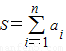最小，在集合A中一定不含有元素ak，使得36＜ak＜72，从而an-1=36；
假设36∉A，根据性质P，对an=72，有ai，aj，使得an=72=ai+aj
显然ai≠aj，所以an+ai+aj=144
而此时集合A中至少还有5个不同于an，ai，aj的元素，
从而S＞（an+ai+aj）+5a1=149，矛盾，
所以36∈A，进而at=36，且an-1=36；
同理可证：an-2=18，an-3=9
（同理可以证明：若18∈A，则an-2=18）．
假设18∉A．
因为an-1=36，根据性质P，有ai，aj，使得an-1=36=ai+aj
显然ai≠aj，所以an+an-1+ai+aj=144，
而此时集合A中至少还有4个不同于an，an-1，ai，aj的元素
从而S＞an+an-1+ai+aj+4a1=148，矛盾，
所以18∈A，且an-2=18
同理可以证明：若9∈A，则an-3=9
假设9∉A
因为an-2=18，根据性质P，有ai，aj，使得an-2=18=ai+aj
显然ai≠aj，所以an+an-1+an-2+ai+aj=144
而此时集合A中至少还有3个不同于an，an-1，an-2，ai，aj的元素
从而S＞an+an-1+an-2+ai+aj+3a1=147，矛盾，
所以9∈A，且an-3=9）
至此，我们得到了an-1=36，an-2=18，an-3=9ai=7，aj=2．
根据性质P，有ai，aj，使得9=ai+aj
我们需要考虑如下几种情形：
①ai=8，aj=1，此时集合中至少还需要一个大于等于4的元素ak，才能得到元素8，
则S＞148；
②，此时集合中至少还需要一个大于4的元素ak，才能得到元素7，
则S＞148；
③ai=6，aj=3，此时集合A={1，2，3，6，9，18，36，72}的和最小，为147；
④ai=5，aj=4，此时集合A={1，2，4，5，9，18，36，72}的和最小，为147．…（14分）
点评：本题考查数列的求和，突出考查反证法的应用，考查分类讨论思想与转化思想，考查构造函数的思想，an-1=36，an-2=18的证明是难点，属于难题．
练习册系列答案
相关题目