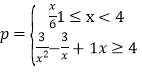题目内容
【题目】![]() 两城相距
两城相距![]() ,在两地之间距
,在两地之间距![]() 城
城![]() 处
处![]() 地建一核电站给
地建一核电站给![]() 两城供电.为保证城市安全,核电站距城市距离不得少于
两城供电.为保证城市安全,核电站距城市距离不得少于![]() .已知供电费用(元)与供电距离(
.已知供电费用(元)与供电距离(![]() )的平方和供电量(亿度)之积成正比,比例系数
)的平方和供电量(亿度)之积成正比,比例系数![]() ,若
,若![]() 城供电量为
城供电量为![]() 亿度/月,
亿度/月,![]() 城为
城为![]() 亿度/月.
亿度/月.
(Ⅰ)把月供电总费用![]() 表示成
表示成![]() 的函数,并求定义域;
的函数,并求定义域;
(Ⅱ)核电站建在距![]() 城多远,才能使供电费用最小,最小费用是多少?
城多远,才能使供电费用最小,最小费用是多少?
【答案】(Ⅰ)![]() ,定义域为
,定义域为![]() ;(Ⅱ)核电站建在距
;(Ⅱ)核电站建在距![]() 城
城![]() 时,才能使供电费用最小,最小费用为
时,才能使供电费用最小,最小费用为![]() 元.
元.
【解析】
试题(Ⅰ)利用供电费用=电价×电量可建立函数,同时根据题设要求写出其定义域;(Ⅱ)根据﹙Ⅰ﹚所得函数的解析式及定义域,通过配方,根据二次函数的性质可求得最值,进而确定电站所建的位置.
试题解析:(Ⅰ)![]() ,即
,即![]() ,
,
由![]() 得
得![]() ,
,
所以函数解析式为![]() ,定义域为
,定义域为![]() .
.
(Ⅱ)由![]() 得
得![]() ,
,
因为![]() 所以
所以![]() 在
在![]() 上单调递增,所以当
上单调递增,所以当![]() 时,
时,![]() .
.
故当核电站建在距![]() 城
城![]() 时,才能使供电费用最小,最小费用为
时,才能使供电费用最小,最小费用为![]() 元.
元.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
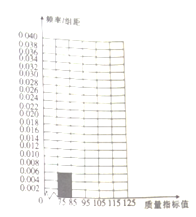
【题目】某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,现用一种新配方做试验,生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
质量指标值 |
|
|
|
|
|
频数 | 6 | 26 | 38 | 22 | 8 |
(1)将答题卡上列出的这些数据的频率分布表填写完整,并补齐频率分布直方图;
(2)估计这种产品质量指标值的平均值(同一组中的数据用该组区间的中点值作代表)与中位数(结果精确到0.1).
质量指标值分组 | 频数 | 频率 |
| 6 | 0.06 |
| ||
| ||
| ||
| ||
合计 | 100 | 1 |