题目内容
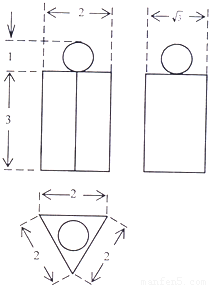
如图所示几何体的三视图,则该三视图的表面积为______
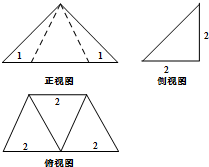

根据三视图知该几何体是四棱锥,底面是等腰梯形,如图所示:
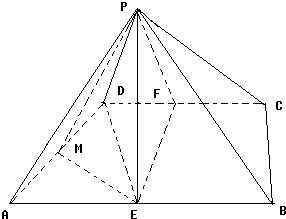
E和F分别是AB和CD中点,作EM⊥AD,连接PM,且PD=PC,
由三视图得,PE⊥底面ABCD,AB=4,CD=2,PE═EF=2
在直角三角形△PEF中,PF=
=2
,
在直角三角形△DEF中,DE=
=
,同理在直角梯形ADEF中,AD=
,
根据△AED的面积相等得,
×AD×ME=
×AE×EF,解得ME=
,
∵PE⊥底面ABCD,EM⊥AD,∴PM⊥AD,PE⊥ME,
在直角三角形△PME中,PM=
=
=
,
∴该四棱锥的全面积S=
×(4+2)×2+
×4×2+
×2×2
+2×
×
×
=16+2
.
故答案为:16+2
.

E和F分别是AB和CD中点,作EM⊥AD,连接PM,且PD=PC,
由三视图得,PE⊥底面ABCD,AB=4,CD=2,PE═EF=2
在直角三角形△PEF中,PF=
| EF2+PF2 |
| 2 |
在直角三角形△DEF中,DE=
| EF2+DF2 |
| 5 |
| 5 |
根据△AED的面积相等得,
| 1 |
| 2 |
| 1 |
| 2 |
| 4 | ||
|
∵PE⊥底面ABCD,EM⊥AD,∴PM⊥AD,PE⊥ME,
在直角三角形△PME中,PM=
| EM2+PE2 |
|
| 6 | ||
|
∴该四棱锥的全面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 5 |
| 6 | ||
|
| 2 |
故答案为:16+2
| 2 |

练习册系列答案
相关题目
 (2012•黄浦区二模)如图所示的几何体,是由棱长为2的正方体ABCD-A1B1C1D1截去一个角后所得的几何体.
(2012•黄浦区二模)如图所示的几何体,是由棱长为2的正方体ABCD-A1B1C1D1截去一个角后所得的几何体.