题目内容
【题目】如图,已知![]() 是上、下底边长为2和6,高为
是上、下底边长为2和6,高为![]() 的等腰梯形,将它沿对称轴
的等腰梯形,将它沿对称轴![]() 折叠,使二面角
折叠,使二面角![]() 为直二面角.
为直二面角.


(1)证明:![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)可以以点![]() 为原点,
为原点, ![]() 为
为![]() 轴建立空间直角坐标系,证明
轴建立空间直角坐标系,证明![]() ,或是证明
,或是证明![]() 平面
平面![]() ,即证明
,即证明![]() ,(2)向量法是分别求两个平面
,(2)向量法是分别求两个平面![]() 和
和![]() 的法向量,求法向量夹角的余弦值.
的法向量,求法向量夹角的余弦值.
试题解析:解法一:(1)证明由题设知![]() ,
,![]() ,所以
,所以![]() 是所折成的直二面角的平面角,即
是所折成的直二面角的平面角,即![]() .
.
故可以![]() 为原点,
为原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
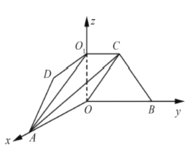
如图,则相关各点的坐标是![]() ,
,![]() ,
,![]() ,
,![]() ,
,
从而![]() ,
,![]() ,
,![]() .
.
所以![]() .
.
(2)因为![]() ,所以
,所以![]() .
.
由(1)![]() ,所以
,所以![]() 平面
平面![]() ,
,![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
设![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
由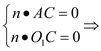
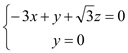 取
取![]() ,得
,得![]() .
.
设二面角![]() 的大小为
的大小为![]() ,由
,由![]() 、
、![]() 的方向可知
的方向可知![]() ,所以
,所以![]()
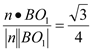 即二面角
即二面角![]() 的余弦值是
的余弦值是![]() .
.
解法二:(1)证明:有题设知![]() ,
,![]() ,
,
所以![]() 是所折成的直二面角的平面角,
是所折成的直二面角的平面角,
即![]() .从而
.从而![]() 平面
平面![]() ,
,
![]() 是
是![]() 在面
在面![]() 内的射影.
内的射影.
因为![]() ,
,![]() ,
,
所以![]() ,
,![]() ,从而
,从而![]() ,
,![]() 平面
平面![]() .
.
可得![]() .
.
(2)由(1)![]() ,
,![]() ,知
,知![]() 平面
平面![]() ,
,
设![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,则
,则![]() 是
是![]() 在平面
在平面![]() 内的射影,由
内的射影,由![]() 平面
平面![]() 可得
可得![]() .
.
所以![]() 是二面角
是二面角![]() 的平面角,
的平面角,
由题设知![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
从而![]() ,又
,又![]() ,
,
所以![]() ,即二面角
,即二面角![]() 的余弦值
的余弦值![]() .
.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
【题目】重庆市某厂党支部10月份开展“两学一做”活动,将10名党员技工平均分为甲,乙两组进行技能比赛.要求在单位时间内每个技工加工零件若干,其中合格零件的个数如下表:
1号 | 2号 | 3号 | 4号 | 5号 | |
甲组 | 4 | 5 | 7 | 9 | 10 |
乙组 | 5 | 6 | 7 | 8 | 9 |
(1)分别求出甲,乙两组技工在单位时间内完成合格零件的平均数及方差,并由此分析两组技工的技术水平;
(2)质检部门从该车间甲,乙两组中各随机抽取1名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过12件,则称该车间“质量合格”,求该车间“质量合格”的概率.