题目内容
在
中，
，动点P的轨迹为曲线E，曲线E过点C且满足|PA|+|PB|为常数。
（1）求曲线E的方程；
（2）是否存在直线L，使L与曲线E交于不同的两点M、N，且线段MN恰被直线
平分？若存在，求出L的斜率的取值范围；若不存在说明理由。
中，，动点P的轨迹为曲线E，曲线E过点C且满足|PA|+|PB|为常数。（1）求曲线E的方程；
（2）是否存在直线L，使L与曲线E交于不同的两点M、N，且线段MN恰被直线
平分？若存在，求出L的斜率的取值范围；若不存在说明理由。（1）略（2）
本试题主要是考查了椭圆方程求解以及直线与椭圆的位置关系的综合运用。
（1）根据已知条件，易知
，又因为
，所以
，
所以
，
由|PA|+|PB|的值为常数知动点P的轨迹为焦点在y轴上的椭圆
（2）联立方程组，结合韦达定理，表示得到参数k的等式，进而求解其范围。
解：（1）易知，又因为，所以，
所以，
由|PA|+|PB|的值为常数知动点P的轨迹为焦点在y轴上的椭圆 ------4分
其中
------6分
（2）假设L存在，因为L与直线相交，所以直线L有斜率，
设L的方程为
----------------7分
由
得
（*） ------9分
因为直线L与椭圆有两个交点
所以（*）的判别式
① -----10分
设
，则
-------------11分
因为MN被直线平分
所以
② ----------12分
把②代入①得
因为
所以
---------------13分
所以
所以
或
即直线L的斜率取值范围是 ------------14分
（1）根据已知条件，易知
，又因为，所以，所以
，由|PA|+|PB|的值为常数知动点P的轨迹为焦点在y轴上的椭圆
（2）联立方程组，结合韦达定理，表示得到参数k的等式，进而求解其范围。
解：（1）易知
，又因为，所以，所以
，由|PA|+|PB|的值为常数知动点P的轨迹为焦点在y轴上的椭圆 ------4分
其中
------6分（2）假设L存在，因为L与直线
相交，所以直线L有斜率，设L的方程为
----------------7分由
得 （*） ------9分因为直线L与椭圆有两个交点
所以（*）的判别式
① -----10分设
，则 -------------11分因为MN被直线
平分所以
② ----------12分把②代入①得
因为
所以 ---------------13分 所以
所以或即直线L的斜率取值范围是
------------14分
练习册系列答案
相关题目
：
的离心率是
，其左、右顶点分别为
，
，
为短轴的端点，△
的面积为
．
为椭圆
是椭圆
，
与直线
分别交于
，
两点，证明：以
为直径的圆与直线
相切于点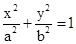
(a＞b＞0)的离心率为
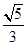,短轴一个端点到右焦点的距离为3.
∈(0,
)，方程
表示焦点在x轴上的椭圆，则
与坐标轴正半轴的两个交点.
为参数，求椭圆的参数方程；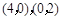
，椭圆的方程是
或
是椭圆的一部分，灯丝位于椭圆的一个焦点
上，片门位于另一个焦点
上，由椭圆一个焦点
，
，
试建立适当的坐标系，求截口
（
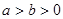）的左顶点， B，C在椭圆E上，若四边形OABC为平行四边形，且∠OAB＝30°，则椭圆E的离心率等于 .