题目内容
已知直线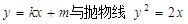 交于A,B两点,且
交于A,B两点,且 (其中O为坐标原点),若OM⊥AB于M,则点M的轨迹方程为 ( )
(其中O为坐标原点),若OM⊥AB于M,则点M的轨迹方程为 ( )
A.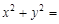 2 B.
2 B.
C.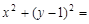 1 D.
1 D.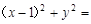 4
4
【答案】
B
【解析】
试题分析:联立直线方程与抛物线方程并整理得 ,
,
设 则
则
因为 ,所以
,所以 ,所以
,所以 ,代入数据可得
,代入数据可得 ,所以直线
,所以直线 ,所以直线恒过定点(2,0),
,所以直线恒过定点(2,0),
因为OM⊥AB,所以 ,整理得
,整理得 即为点M的轨迹方程.
即为点M的轨迹方程.
考点:本小题主要考查直线与抛物线的性质,向量的运算,直线过定点,轨迹问题.
点评:解决本小题的关键是根据 可得
可得 ,从而利用韦达定理知道
,从而利用韦达定理知道 ,本小题运算量比较大,要仔细运算,另外要注意直线过定点问题.
,本小题运算量比较大,要仔细运算,另外要注意直线过定点问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目