题目内容
已知函数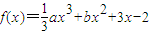 ,其中a≠0
,其中a≠0(1)若a=1,且f(x)的导函数的图象关于直线x=2对称时.试求f(x)在区间[0,2]上的最小值.
(2)若a>0,且f(x)在区间(0,1]上单调递增,试用a表示出b的取值范围.
【答案】分析:(1)先求出f′(x),把a=1时代入到导函数中,然后因为f(x)的导函数的图象关于直线x=2对称得到b的值,确定出函数解析式.在区间[0,2]上讨论函数的增减性,判断求得函数的最小值;
(2)由f(x)在区间(0,1]上单调递增得到导函数大于0,ax2+2bx+3>0,?x∈(0,1]恒成立2bx>-ax2-3即2b> =-(ax+
=-(ax+ ),设y=ax+
),设y=ax+ ,讨论a的取值求出y的最小值即可得到b的取值范围.
,讨论a的取值求出y的最小值即可得到b的取值范围.
解答:解:f′(x)=ax2+2bx+3(2分)
(1)∵a=1
∴f′(x)=x2+2bx+3=(x+b)2+3-b2,
f(x)的导函数的图象关于直线x=2对称
∴b=-2,f′(x)=x2-4x+3=(x-1)(x-3)(4分)

f(x)在区间[0,2]上的最小值=min{ (7分)
(7分)
(2)由a>0,且f(x)在区间(0,1]上单调递增,
知:ax2+2bx+3>0,?x∈(0,1]恒成立2bx>-ax2-3
∵ (10分)
(10分)
为求最大值,先以下求函数 的最小值
的最小值
当 时,y′(x)在
时,y′(x)在 上为负,在
上为负,在 为正,
为正,
即y(x)在 上递减,在
上递减,在 递增y(x)的最小值是
递增y(x)的最小值是
当 时,y′(x)在区间(0,1]上恒为负,
时,y′(x)在区间(0,1]上恒为负,
即y(x)在区间(0,1]上单调递减,所以y(x)的最小值是y(1)=a+3(13分)
经检验,以上端点值也符合.
综上所述,当a>3时,b的取值范围是
当0<a≤3时b的取值范围是 (15分)
(15分)
点评:考查学生利用导数研究函数单调性的能力,利用导数求闭区间上函数最值的能力.以及理解不等式恒成立时所取的条件.
(2)由f(x)在区间(0,1]上单调递增得到导函数大于0,ax2+2bx+3>0,?x∈(0,1]恒成立2bx>-ax2-3即2b>
 =-(ax+
=-(ax+ ),设y=ax+
),设y=ax+ ,讨论a的取值求出y的最小值即可得到b的取值范围.
,讨论a的取值求出y的最小值即可得到b的取值范围.解答:解:f′(x)=ax2+2bx+3(2分)
(1)∵a=1
∴f′(x)=x2+2bx+3=(x+b)2+3-b2,
f(x)的导函数的图象关于直线x=2对称
∴b=-2,f′(x)=x2-4x+3=(x-1)(x-3)(4分)

f(x)在区间[0,2]上的最小值=min{
 (7分)
(7分)(2)由a>0,且f(x)在区间(0,1]上单调递增,
知:ax2+2bx+3>0,?x∈(0,1]恒成立2bx>-ax2-3
∵
 (10分)
(10分)为求最大值,先以下求函数
 的最小值
的最小值
当
 时,y′(x)在
时,y′(x)在 上为负,在
上为负,在 为正,
为正,即y(x)在
 上递减,在
上递减,在 递增y(x)的最小值是
递增y(x)的最小值是
当
 时,y′(x)在区间(0,1]上恒为负,
时,y′(x)在区间(0,1]上恒为负,即y(x)在区间(0,1]上单调递减,所以y(x)的最小值是y(1)=a+3(13分)
经检验,以上端点值也符合.
综上所述,当a>3时,b的取值范围是

当0<a≤3时b的取值范围是
 (15分)
(15分)点评:考查学生利用导数研究函数单调性的能力,利用导数求闭区间上函数最值的能力.以及理解不等式恒成立时所取的条件.

练习册系列答案
相关题目
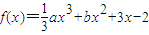 ,其中a≠0
,其中a≠0 =
= ,其中a≠0.
,其中a≠0. ,
,
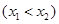 ,记直线AB的斜率为K,问:是否存在x0∈(x1,x2),使
,记直线AB的斜率为K,问:是否存在x0∈(x1,x2),使 成立?若存在,求
成立?若存在,求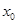 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. =
=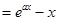 ,其中a≠0
,其中a≠0 ,
,
 ,记直线AB的斜率为K,问:是否存在x0∈(x1,x2),使
,记直线AB的斜率为K,问:是否存在x0∈(x1,x2),使 成立?若存在,求
成立?若存在,求 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
 ,其中a≠0。
,其中a≠0。 ≥1恒成立,求a的取值集合。
≥1恒成立,求a的取值集合。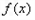 的图像上取定两点
的图像上取定两点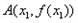 ,
,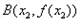
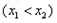 ,记直线AB的斜率为K,问:是否存在x0∈(x1,x2),使
,记直线AB的斜率为K,问:是否存在x0∈(x1,x2),使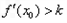 成立?若存在,求
成立?若存在,求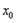 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。