Question

（本小题满分12分）已知圆C的圆心在直线y=2x上，且与直线l：x+y+1=0相切于点P（-1,0）.

（Ⅰ）求圆C的方程；

（Ⅱ）若A（1,0），点B是圆C上的动点，求线段AB中点M的轨迹方程，并说明表示什么曲线.

 

Answer 1

【答案】

（Ⅰ）圆C：；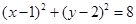

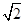（Ⅱ），表示以（1,1）为圆心，为半径的圆.

【解析】

试题分析：）设圆心C（a，b）半径为r,要求圆心的方程需要建立关于a,b,r的三个方程，因为圆心在直线y=2x上,所以b=2a, 又C落在过P且垂直于l的直线y=x+1上,所以b=a+1,

又因为r=|CP|,从而可求出a,b,r的值.

(II)本小题属于相关点法求动点的轨迹方程，设M（x，y），B（x₀，y₀），则有，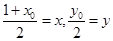

可得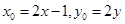，然后将B的坐标代入圆C的方程即可得到M的轨迹方程，再通过方程可判断出M的轨迹也是圆.

（Ⅰ）设圆心C（a，b）半径为r，则有b=2a，…………………1分

又C落在过P且垂直于l的直线y=x+1上，…………………3分

故有b=a+1，解得a=1，b=2，从而r=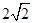…………………5分

∴圆C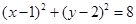：……………………………………6分

（Ⅱ）设M（x，y），B（x₀，y₀），则有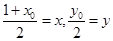，……………………8分

解得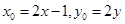，代入圆C方程得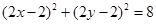，…………10分

化简得……………11分

表示以（1,1）为圆心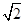，为半径的圆.………12分

考点：求圆的方程，相关点法求轨迹方程.

点评：求圆的方程无论是设圆的标准方程还是设圆的一般方程都要从题目中找到三个方程条件求解，要注意圆的几何性质的应用.用相关点法求轨迹方程时，要注意把相关点的坐标用动点的坐标表示出来，然后代入相关点所满足的方程即可得到所求动点的轨迹方程.