题目内容
给出下列命题：
①若f（tanx）=sin2x，则f（-1）=-1；
②将函数y=sin(2x+
)的图象向右平移
个单位，得到y=sin2x的图象；
③方程sinx=lgx有三个实数根；
④函数y=1-2cosx-2sin2x的值域是-
≤y≤3
⑤把y=cosx+cos(
+x)写成一个角的正弦形式是y=
sin(
+x)
其中正确的命题的序号是______（要求写出所有正确命题的序号）．
①若f（tanx）=sin2x，则f（-1）=-1；
②将函数y=sin(2x+
| π |
| 3 |
| π |
| 3 |
③方程sinx=lgx有三个实数根；
④函数y=1-2cosx-2sin2x的值域是-
| 3 |
| 2 |
⑤把y=cosx+cos(
| π |
| 3 |
| 3 |
| π |
| 3 |
其中正确的命题的序号是______（要求写出所有正确命题的序号）．
①由题得tanx=-1所以x=
+kπ所以2x=
+2kπ所以sin2x=-1，故①正确．
②由左加右减得：将函数y=sin(2x+
)的图象向右平移
个单位得y=sin(2x-
)故答案②错误．
③即函数y=sinx与函数y=lgx有三个交点，因为函数y=lgx过点（10，1）且函数y=sinx是周期函数，故③正确．
④原函数为y=2cos2x-2cosx-1，还原的y=2t2-2t-1，t∈[-1，1]，所以函数的值域是-
≤y≤3，故④正确．
⑤y=cosx+cos(
+x)化简结果是y=
sin(
-x)，故⑤错误．
故答案为：①③④．
| 3π |
| 4 |
| 3π |
| 2 |
②由左加右减得：将函数y=sin(2x+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
③即函数y=sinx与函数y=lgx有三个交点，因为函数y=lgx过点（10，1）且函数y=sinx是周期函数，故③正确．
④原函数为y=2cos2x-2cosx-1，还原的y=2t2-2t-1，t∈[-1，1]，所以函数的值域是-
| 3 |
| 2 |
⑤y=cosx+cos(
| π |
| 3 |
| 3 |
| π |
| 3 |
故答案为：①③④．
练习册系列答案
相关题目
＞0，则f(x)＞0；
dx＝4；
＝
．
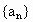成等比数列，
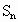是前n项和，则
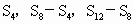成等比数列；
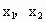，若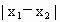
的最小值为π，则ω的值为2，θ的值为
；
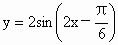的图象的一个对称点是
．