题目内容

一个正三角形的顶点都在抛物线y²=4x上，其中一个顶点在坐标原点，这个三角形的面积是

A.
$数学公式$
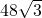
B.
$数学公式$
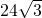
C.
$数学公式$
D.
$数学公式$

A
分析：根据抛物线方程先设其中一个顶点是（x，2 $\text{[math]}$ ），根据正三角形的性质 $\text{[math]}$ =tan30°= $\text{[math]}$ 求得x，进而可得另两个顶点坐标，最后根据面积公式求得答案．
解答：设其中一个顶点是（x，2 $\text{[math]}$ ）
因为是正三角形
所以 $\text{[math]}$ =tan30°= $\text{[math]}$
即 $\text{[math]}$
解得x=12
所以另外两个顶点是（12，4 $\text{[math]}$ ）与（12，-4 $\text{[math]}$ ）
三角形的面积12•（4 $\text{[math]}$ +4 $\text{[math]}$ ） $\text{[math]}$ =48 $\text{[math]}$
故选A
点评：本题主要考查抛物线的应用．利用抛物线性质解决解三角形问题．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

名校名师夺冠金卷系列答案

小学英语课时练系列答案

培优新帮手系列答案

天天向上一本好卷系列答案

小学生10分钟应用题系列答案

课堂作业广西教育出版社系列答案

相关题目

一个正三角形的三个顶点都在双曲线x²-ay²=1的右支上，其中一个顶点与双曲线右顶点重合，则实数a的取值范围是

一个正三角形的顶点都在抛物线y²=4x上，其中一个顶点在坐标原点，这个三角形的面积是（　　）

一个正三角形的三个顶点都在双曲线x²-ay²=1的右支上，其中一个顶点是双曲线的右顶点，求实数a的取值范围．

一个正三角形的顶点都在抛物线y²=4x上，其中一个顶点在坐标原点，这个三角形的面积是（）
A．