题目内容
函数f （x）=log
cos(
x+
)的单调递增区间为
| 1 |
| 2 |
| 1 |
| 3 |
| π |
| 4 |
(6kπ-
，6kπ+
)，k∈Z
| 3π |
| 4 |
| 3π |
| 4 |
(6kπ-
，6kπ+
)，k∈Z
．| 3π |
| 4 |
| 3π |
| 4 |
分析：利用复合函数的单调性的规律：同增异减将原函数的单调性转化为t的单调性，利用三角函数的单调性的处理方法：整体数学求出单调区间．
解答：解：∵y=log0.5t为减函数，
所以函数f （x）=log
cos(
x+
)的单调递增区间为即为 t=cos(
x+
)单调减区间
且t=cos(
x+
)＞0
令2kπ＜
x+
＜2kπ+
解得6kπ-
＜x＜6kπ+
故答案为(6kπ-
，6kπ+
) （k∈Z）
所以函数f （x）=log
| 1 |
| 2 |
| 1 |
| 3 |
| π |
| 4 |
| 1 |
| 3 |
| π |
| 4 |
且t=cos(
| 1 |
| 3 |
| π |
| 4 |
令2kπ＜
| 1 |
| 3 |
| π |
| 4 |
| π |
| 2 |
解得6kπ-
| 3π |
| 4 |
| 3π |
| 4 |
故答案为(6kπ-
| 3π |
| 4 |
| 3π |
| 4 |
点评：本题考查复合函数的单调性的规律、三角函数的单调区间的求法．
练习册系列答案
尖子生新课堂课时作业系列答案
相关题目
的定义域为M，g(x)＝lo
(2＋x＝6x2)的单调递减区间是开区间N，设全集U＝R，则M∩CU(N)＝________．
）2+7lo
+3≤0的解集为M，求当x∈M时，函数f（x）=（lo
）（lo
）的最大值和最小值．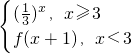
，则f（2+lo
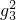）的值为________．