题目内容
等腰Rt△ACB,AB=2,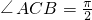 .以直线AC为轴旋转一周得到一个圆锥,D为圆锥底面一点,BD⊥CD,CH⊥AD于点H,M为AB中点,则当三棱锥C-HAM的体积最大时,CD的长为
.以直线AC为轴旋转一周得到一个圆锥,D为圆锥底面一点,BD⊥CD,CH⊥AD于点H,M为AB中点,则当三棱锥C-HAM的体积最大时,CD的长为
- A.

- B.
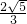
- C.

- D.

C
分析:根据题意,结合线面垂直的判定与性质,证出AB⊥平面CMH,从而AM是三棱锥C-HAM的高,得VC-HAM= S△CMH×AM,因此当S△CMH达到最大值时,三棱锥C-HAM的体积最大.设∠BCD=θ,利用Rt△ACD中等积转换和Rt△ABD∽Rt△AHM,算出CH、HM关于θ的式子,从而得到S△CMH=
S△CMH×AM,因此当S△CMH达到最大值时,三棱锥C-HAM的体积最大.设∠BCD=θ,利用Rt△ACD中等积转换和Rt△ABD∽Rt△AHM,算出CH、HM关于θ的式子,从而得到S△CMH= CH•HM=
CH•HM= ,最后根据基本不等式得当tanθ=
,最后根据基本不等式得当tanθ= 时,S△CMH达到最大值,根据同角三角函数的基本关系算出cosθ=
时,S△CMH达到最大值,根据同角三角函数的基本关系算出cosθ= ,从而得出CD的长为
,从而得出CD的长为 ,即为当三棱锥C-HAM的体积最大时CD的长.
,即为当三棱锥C-HAM的体积最大时CD的长.
解答: 根据题意,得
根据题意,得
∵AC⊥平面BCD,BD?平面BCD,∴AC⊥BD,
∵CD⊥BD,AC∩CD=C,∴BD⊥平面ACD,可得BD⊥CH,
∵CH⊥AD,AD∩BD=D,∴CH⊥平面ABD,可得CH⊥AB,
∵CM⊥AB,CH∩CM=C,∴AB⊥平面CMH,
因此,三棱锥C-HAM的体积V= S△CMH×AM=
S△CMH×AM= S△CMH
S△CMH
由此可得,当S△CMH达到最大值时,三棱锥C-HAM的体积最大
设∠BCD=θ,则Rt△BCD中,BC= AB=
AB=
可得CD= ,BD=
,BD=
Rt△ACD中,根据等积转换得CH= =
=
Rt△ABD∽Rt△AHM,得 ,所以HM=
,所以HM= =
=
因此,S△CMH= CH•HM=
CH•HM= =
=
∵4+2tan2θ≥4 tanθ,
tanθ,
∴S△CMH= ≤
≤ =
= ,
,
当且仅当tanθ= 时,S△CMH达到最大值,三棱锥C-HAM的体积同时达到最大值.
时,S△CMH达到最大值,三棱锥C-HAM的体积同时达到最大值.
∵tanθ= >0,可得sinθ=
>0,可得sinθ= cosθ>0
cosθ>0
∴结合sin2θ+cos2θ=1,解出cos2θ= ,可得cosθ=
,可得cosθ= (舍负)
(舍负)
由此可得CD= =
= ,
,
即当三棱锥C-HAM的体积最大时,CD的长为
故选:C
点评:本题给出旋转体中,求三棱锥的体积最大值时CD的长,着重考查了线面垂直的判定与性质、基本不等式求最值、相似三角形中比例线段的计算和同角三角函数基本关系等知识,属于中档题.
分析:根据题意,结合线面垂直的判定与性质,证出AB⊥平面CMH,从而AM是三棱锥C-HAM的高,得VC-HAM=
 S△CMH×AM,因此当S△CMH达到最大值时,三棱锥C-HAM的体积最大.设∠BCD=θ,利用Rt△ACD中等积转换和Rt△ABD∽Rt△AHM,算出CH、HM关于θ的式子,从而得到S△CMH=
S△CMH×AM,因此当S△CMH达到最大值时,三棱锥C-HAM的体积最大.设∠BCD=θ,利用Rt△ACD中等积转换和Rt△ABD∽Rt△AHM,算出CH、HM关于θ的式子,从而得到S△CMH= CH•HM=
CH•HM= ,最后根据基本不等式得当tanθ=
,最后根据基本不等式得当tanθ= 时,S△CMH达到最大值,根据同角三角函数的基本关系算出cosθ=
时,S△CMH达到最大值,根据同角三角函数的基本关系算出cosθ= ,从而得出CD的长为
,从而得出CD的长为 ,即为当三棱锥C-HAM的体积最大时CD的长.
,即为当三棱锥C-HAM的体积最大时CD的长.解答:
 根据题意,得
根据题意,得∵AC⊥平面BCD,BD?平面BCD,∴AC⊥BD,
∵CD⊥BD,AC∩CD=C,∴BD⊥平面ACD,可得BD⊥CH,
∵CH⊥AD,AD∩BD=D,∴CH⊥平面ABD,可得CH⊥AB,
∵CM⊥AB,CH∩CM=C,∴AB⊥平面CMH,
因此,三棱锥C-HAM的体积V=
 S△CMH×AM=
S△CMH×AM= S△CMH
S△CMH由此可得,当S△CMH达到最大值时,三棱锥C-HAM的体积最大
设∠BCD=θ,则Rt△BCD中,BC=
 AB=
AB=
可得CD=
 ,BD=
,BD=
Rt△ACD中,根据等积转换得CH=
 =
=
Rt△ABD∽Rt△AHM,得
 ,所以HM=
,所以HM= =
=
因此,S△CMH=
 CH•HM=
CH•HM= =
=
∵4+2tan2θ≥4
 tanθ,
tanθ,∴S△CMH=
 ≤
≤ =
= ,
,当且仅当tanθ=
 时,S△CMH达到最大值,三棱锥C-HAM的体积同时达到最大值.
时,S△CMH达到最大值,三棱锥C-HAM的体积同时达到最大值.∵tanθ=
 >0,可得sinθ=
>0,可得sinθ= cosθ>0
cosθ>0∴结合sin2θ+cos2θ=1,解出cos2θ=
 ,可得cosθ=
,可得cosθ= (舍负)
(舍负)由此可得CD=
 =
= ,
,即当三棱锥C-HAM的体积最大时,CD的长为

故选:C
点评:本题给出旋转体中,求三棱锥的体积最大值时CD的长,着重考查了线面垂直的判定与性质、基本不等式求最值、相似三角形中比例线段的计算和同角三角函数基本关系等知识,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 .以直线AC为轴旋转一周得到一个圆锥,D为圆锥底面一点,BD⊥CD,CH⊥AD于点H,M为AB中点,则当三棱锥C-HAM的体积最大时,CD的长为( )
.以直线AC为轴旋转一周得到一个圆锥,D为圆锥底面一点,BD⊥CD,CH⊥AD于点H,M为AB中点,则当三棱锥C-HAM的体积最大时,CD的长为( )


