题目内容
已知数列{an}满足a1=1，an-an-1=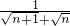
（n≥2），则an=________
-
+1分析：由题意知an-an-1=
，（n≥2），由此可知an=a1+（a2-a1）+（a3-a2）+（a4-a3）+…+（an-an-1）=1+
+（
）+（
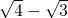）+…+（），从而得到an的值．解答：∵an-an-1=
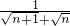=，（n≥2），∴a1=1，
，
，
，…，an-an-1=，∴an=a1+（a2-a1）+（a3-a2）+（a4-a3）+…+（an-an-1）
=1+
+（）+（）+…+（）=
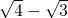．答案：
．点评：本题考查数列的性质和应用，解题时要认真审题，仔细解答．
练习册系列答案
相关题目