题目内容
【题目】已知![]() ,
, ![]() ,曲线
,曲线![]() 上的任意一点
上的任意一点![]() 满足:
满足: ![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() ,
, ![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,设
点,设![]() ,
, ![]() ,试问
,试问![]() 是否为定值?如果是定值,请求出这个定值,如果不是定值,请说明理由.
是否为定值?如果是定值,请求出这个定值,如果不是定值,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(Ⅰ)求出向量的坐标,利用条件化简,即可求点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)分类讨论,利用![]() ,
, ![]() ,结合韦达定理,即可得出结论.
,结合韦达定理,即可得出结论.
试题解析:(1)设![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
,
∵![]() ,∴
,∴![]() ,
,
化简得, ![]() 为所求点
为所求点![]() 的轨迹方程.
的轨迹方程.
(2)设![]() ,
, ![]() .
.
①当直线![]() 与
与![]() 轴不重合时,设直线
轴不重合时,设直线![]() 的方程为
的方程为![]() ,
,
则![]() ,从而
,从而![]() ,
, ![]() ,由
,由![]() 得
得
![]() ,
, ![]() ,
, ![]() ,
,
同理由![]() 得
得![]() ,
,
∴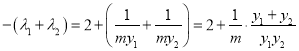 .①
.①
由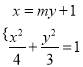 ,得
,得![]() .
.
∴![]() ,
, ![]() ,
,
代入①式得![]() ,∴
,∴![]() .
.
②当直线![]() 与
与![]() 轴重合时,
轴重合时, ![]() ,
, ![]() ,
, ![]() .
.
由![]() ,
, ![]() ,得
,得![]() ,
, ![]() ,∴
,∴![]() ,
,
综上, ![]() 为定值
为定值![]() .
.
点睛:定点、定值问题通常是通过设参数或取特殊值来确定“定点”是什么、“定值”是多少,或者将该问题涉及的几何式转化为代数式或三角问题,证明该式是恒定的. 定点、定值问题同证明问题类似,在求定点、定值之前已知该值的结果,因此求解时应设参数,运用推理,到最后必定参数统消,定点、定值显现.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目