题目内容
已知等比数列{an}的前n项和为Sn,若a3= ,S3=
,S3= ,则a1的值为 .
,则a1的值为 .
【答案】分析:设出等比数列的首项和公比,分公比q等于1和不等于1两种情况列式求首项,公比等于1时,三倍的a1即为前三项的和,公比不等于1时用等比数列前n项和公式写出前三项的和.
解答:解:设等比数列{an}的首项为a1,公比为q,
若q=1,由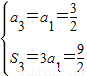 ,得:
,得: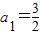
若q≠1,则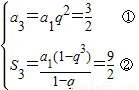 ,
,
由①得: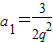 ,代入②得:
,代入②得: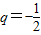 ,代入①得:a1=6
,代入①得:a1=6
所以a1的值为 或6.
或6.
故答案为 或6.
或6.
点评:本题考查了等比数列的前n项和,考查了分类讨论思想,等比数列的前n项和公式只有在公比不等于1时成立,公比等于时,Sn=na1,此题为基础题.
解答:解:设等比数列{an}的首项为a1,公比为q,
若q=1,由
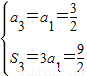 ,得:
,得: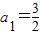
若q≠1,则
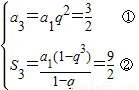 ,
,由①得:
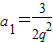 ,代入②得:
,代入②得: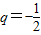 ,代入①得:a1=6
,代入①得:a1=6所以a1的值为
 或6.
或6.故答案为
 或6.
或6.点评:本题考查了等比数列的前n项和,考查了分类讨论思想,等比数列的前n项和公式只有在公比不等于1时成立,公比等于时,Sn=na1,此题为基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目