题目内容
9.已知数列{an}是公比大于1的等比数列,且a102=a15,Sn=a1+a2+…+an,Tn=$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$,求满足Sn>Tn的最小正整数n.分析 设等比数列的首项为a,公比为q,且q>1,运用等比数列的通项公式,可得aq4=1,运用求和公式,化简Sn,
Tn,再由指数函数的单调性,解不等式即可得到n的最小值.
解答 解:设等比数列的首项为a,公比为q,且q>1,
由a102=a15,可得a2q18=aq14,化简得aq4=1,
Sn=a1+a2+…+an=$\frac{a(1-{q}^{n})}{1-q}$=$\frac{a({q}^{n}-1)}{q-1}$,
Tn=$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$=$\frac{\frac{1}{a}(1-\frac{1}{{q}^{n}})}{1-\frac{1}{q}}$=$\frac{q({q}^{n}-1)}{a{q}^{n}(q-1)}$,
由Sn>Tn,可得a>$\frac{q}{a{q}^{n}}$,
即有a2>q1-n,
即为q-8>q1-n,
由q>1可得-8>1-n,
即有n>9,
则满足Sn>Tn的最小正整数n是10.
点评 本题考查等比数列的通项和求和公式的运用,同时考查指数函数的单调性的运用和不等式的解法,属于中档题.

练习册系列答案
相关题目
19.设F1、F2是双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1的两个焦点,点P在双曲线上,且$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,则|$\overrightarrow{P{F}_{1}}$|•|$\overrightarrow{P{F}_{2}}$|的值为( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 8 |
20.曲线x2+y2=1经过伸缩变换$\left\{\begin{array}{l}{x′=\frac{1}{5}x}\\{y′=\frac{1}{3}y}\end{array}\right.$后,变成的曲线方程是( )
| A. | 25x2+9y2=1 | B. | 9x2+25y2=1 | C. | 25x+9y=1 | D. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1 |
18.已知等差数列{an}的通项公式an=2-2n,则它的公差为( )
| A. | -2 | B. | 3 | C. | 2 | D. | -3 |
19.从3名女同学和2名男同学中选1人主持本班的某次主题班会,则不同的选法为( )
| A. | 3 | B. | 5 | C. | 6 | D. | 10 |
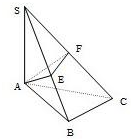 如图,已知SA⊥平面ABC,AB⊥BC,过点A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F
如图,已知SA⊥平面ABC,AB⊥BC,过点A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F