题目内容
一个半径为1的小球在一个内壁棱长为 的正四面体封闭容器内可向各个方向自由运动,则该小球表面永远不可能接触到的容器内壁的面积是 .
的正四面体封闭容器内可向各个方向自由运动,则该小球表面永远不可能接触到的容器内壁的面积是 .
解析试题分析:如图甲,考虑小球挤在一个角时的情况,记小球半径为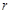 ,作平面
,作平面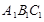 //平面
//平面 ,与小球相切于点
,与小球相切于点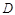 ,则小球球心
,则小球球心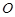 为正四面体
为正四面体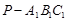 的中心,
的中心,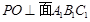 ,垂足
,垂足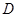 为
为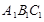 的中心.
的中心.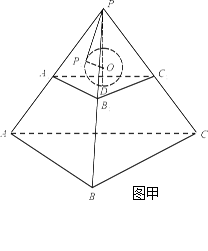
因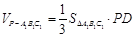
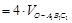
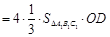 ,
,
故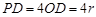 ,从而
,从而 .
.
记此时小球与面 的切点为
的切点为 ,连接
,连接 ,则
,则 .
.
考虑小球与正四面体的一个面(不妨取为 )相切时的情况,易知小球在面
)相切时的情况,易知小球在面 上最靠近边的切点的轨迹仍为正三角形,记为
上最靠近边的切点的轨迹仍为正三角形,记为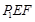 ,如图乙.记正四面体的棱长为
,如图乙.记正四面体的棱长为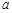 ,过
,过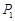 作
作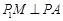 于
于 .
.
因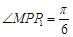 ,有
,有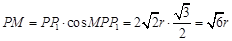 ,故小三角形的边长
,故小三角形的边长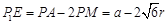 .
.
小球与面 不能接触到的部分的面积为(如答图2中阴影部分)
不能接触到的部分的面积为(如答图2中阴影部分)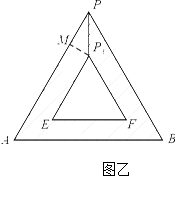

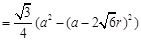
 .
.
又 ,
,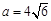 ,所以
,所以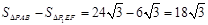 .
.
由对称性,且正四面体共4个面,所以小球不能接触到的容器内壁的面积共为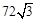 .
.
考点:(1)三棱锥的体积公式;(2)分情况讨论及割补思想的应用。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知四面体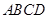 中,
中,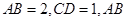 与
与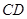 间的距离与夹角分别为3与
间的距离与夹角分别为3与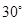 ,则四面体
,则四面体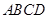 的体积为( )
的体积为( )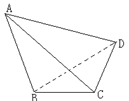
A.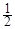 | B.1 | C.2 | D.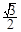 |
 的值为 .
的值为 .

 的圆,且这个几何体是实心球体的一部分,则这个几何体的表面积为 .
的圆,且这个几何体是实心球体的一部分,则这个几何体的表面积为 .
 的正三角形,俯视图是边长为
的正三角形,俯视图是边长为 的正六边形,则该几何体左视图的面积是 。
的正六边形,则该几何体左视图的面积是 。
