题目内容
已知数列{an}是首项为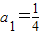 ,公比
,公比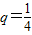 的等比数列,设
的等比数列,设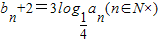 ,数列{cn}满足cn=an•bn.
,数列{cn}满足cn=an•bn.(1)求证:{bn}是等差数列;
(2)求数列{cn}的前n项和Sn;
(3)若
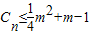 对一切正整数n恒成立,求实数m的取值范围.
对一切正整数n恒成立,求实数m的取值范围.
【答案】分析:(1)根据等比数列的通项公式可求得an,代入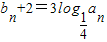 求得bn+1-bn为常数,进而判断出数列{bn}是等差数列.
求得bn+1-bn为常数,进而判断出数列{bn}是等差数列.
(2)由(1)可分别求得an和bn,进而求得Cn进而用错位相减法进行求和.
(3)把(2)中的Cn,代入Cn+1-Cn结果小于0,进而判断出当n≥2时,Cn+1<Cn,进而可推断出当n=1时,Cn取最大值,问题转化为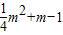 ≥
≥ ,求得m的取值范围.
,求得m的取值范围.
解答:解:(1)由题意知,an=( )n.
)n.
∵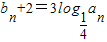 ,
,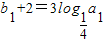
∴b1=1
∴bn+1-bn=3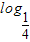 an+1=3
an+1=3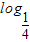 an=3
an=3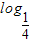
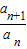 =3
=3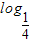 q=3
q=3
∴数列{bn}是首项为1,公差为3的等差数列.
(2)由(1)知,an=( )n.bn=3n-2
)n.bn=3n-2
∴Cn=(3n-2)×( )n.
)n.
∴Sn=1× +4×(
+4×( )2+…+(3n-2)×(
)2+…+(3n-2)×( )n,
)n,
于是 Sn=1×(
Sn=1×( )2+4×(
)2+4×( )3+…(3n-2)×(
)3+…(3n-2)×( )n+1,
)n+1,
两式相减得 Sn=
Sn= +3×[(
+3×[( )2+(
)2+( )3+…+(
)3+…+( )n)-(3n-2)×(
)n)-(3n-2)×( )n+1,
)n+1,
= -(3n-2)×(
-(3n-2)×( )n+1,
)n+1,
∴Sn= -
-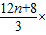 (
( )n+1
)n+1
(3)∵Cn+1-Cn=(3n+1)×( )n+1-(3n-2)×(
)n+1-(3n-2)×( )n=9(1-n)×(
)n=9(1-n)×( )n+1,
)n+1,
∴当n=1时,C2=C1=
当n≥2时,Cn+1<Cn,即C2=C1>C3>C4<…>Cn
∴当n=1时,Cn取最大值是
又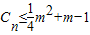
∴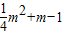 ≥
≥
即m2+4m-5≥0解得m≥1或m≤-5.
点评:本题主要考查了等差数列和等比数列的性质,裂项法求和,解不等式等问题.
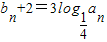 求得bn+1-bn为常数,进而判断出数列{bn}是等差数列.
求得bn+1-bn为常数,进而判断出数列{bn}是等差数列.(2)由(1)可分别求得an和bn,进而求得Cn进而用错位相减法进行求和.
(3)把(2)中的Cn,代入Cn+1-Cn结果小于0,进而判断出当n≥2时,Cn+1<Cn,进而可推断出当n=1时,Cn取最大值,问题转化为
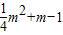 ≥
≥ ,求得m的取值范围.
,求得m的取值范围.解答:解:(1)由题意知,an=(
 )n.
)n.∵
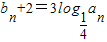 ,
,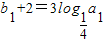
∴b1=1
∴bn+1-bn=3
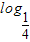 an+1=3
an+1=3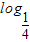 an=3
an=3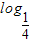
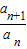 =3
=3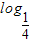 q=3
q=3∴数列{bn}是首项为1,公差为3的等差数列.
(2)由(1)知,an=(
 )n.bn=3n-2
)n.bn=3n-2∴Cn=(3n-2)×(
 )n.
)n.∴Sn=1×
 +4×(
+4×( )2+…+(3n-2)×(
)2+…+(3n-2)×( )n,
)n,于是
 Sn=1×(
Sn=1×( )2+4×(
)2+4×( )3+…(3n-2)×(
)3+…(3n-2)×( )n+1,
)n+1,两式相减得
 Sn=
Sn= +3×[(
+3×[( )2+(
)2+( )3+…+(
)3+…+( )n)-(3n-2)×(
)n)-(3n-2)×( )n+1,
)n+1,=
 -(3n-2)×(
-(3n-2)×( )n+1,
)n+1,∴Sn=
 -
-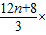 (
( )n+1
)n+1(3)∵Cn+1-Cn=(3n+1)×(
 )n+1-(3n-2)×(
)n+1-(3n-2)×( )n=9(1-n)×(
)n=9(1-n)×( )n+1,
)n+1,∴当n=1时,C2=C1=

当n≥2时,Cn+1<Cn,即C2=C1>C3>C4<…>Cn
∴当n=1时,Cn取最大值是

又
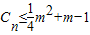
∴
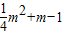 ≥
≥
即m2+4m-5≥0解得m≥1或m≤-5.
点评:本题主要考查了等差数列和等比数列的性质,裂项法求和,解不等式等问题.

练习册系列答案
相关题目