题目内容
18.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F(c,0),右顶点为A(a,0),过F作x轴的垂线与双曲线交于B,C两点,过B,C分别作AC,AB的垂线,两垂线交于点D.,若D到直线BC的距离等于a+c,则双曲线的离心率为$\sqrt{2}$.分析 由题意可得D为△ABC的垂心,求得D(-a,0),再由两直线垂直的条件:斜率之积为-1,计算即可得到a=b,由离心率公式即可得到所求.
解答 解:由题意可得D为△ABC的垂心,
即有AD⊥BC,即D在x轴上,
由D到直线BC的距离等于a+c,
则D(-a,0),
令x=c,可得y2=b2($\frac{{c}^{2}}{{a}^{2}}$-1),
解得y=±$\frac{{b}^{2}}{a}$,
可设B(c,$\frac{{b}^{2}}{a}$),C(c,-$\frac{{b}^{2}}{a}$),
由BD⊥AC,可得kBD•kAC=-1,
即$\frac{\frac{{b}^{2}}{a}}{c+a}$•$\frac{-\frac{{b}^{2}}{a}}{c-a}$=-1,
化简可得a=b,即有c=$\sqrt{2}$a,
e=$\frac{c}{a}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查双曲线的方程和性质,考查三角形的垂心的概念,以及两直线垂直的条件,考查运算能力,属于中档题.

练习册系列答案
相关题目
6.已知双曲线的中心在原点,焦点在x轴上,若其渐进线与圆x2+y2-6y+3=0相切,则此双曲线的离心率等于( )
| A. | $\frac{1}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\sqrt{6}$ |
13.一艘船以20km/h的速度向正北航行,船在A处看见灯塔B在船的东北方向,1h后船在C处看见灯塔B在船的北偏东75°的方向上,这时船与灯塔的距离BC等于( )
| A. | 20$\sqrt{2}$ | B. | 20 | C. | 20$\sqrt{3}$ | D. | 10$\sqrt{2}$ |
3.某空间几何体的三视图(单位:cm)如图所示,则此几何体的体积为( )
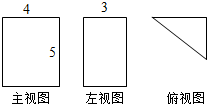

| A. | 10 | B. | 15 | C. | 20 | D. | 30 |
10.如图在边长为1的正方形网格中用粗线画出了某个多面体的三视图,则该多面体的表面积为( )
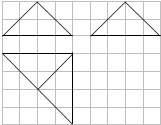

| A. | 8+12$\sqrt{2}$ | B. | 16+24$\sqrt{2}$ | C. | $\frac{1}{3}(8+12\sqrt{2})$ | D. | 4+6$\sqrt{2}$ |
7.某几何体的正(主)视图和侧(左)视图如图所示,则该几何体的体积不可能是( )
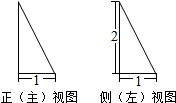

| A. | $\frac{1}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{2}{3}$ | D. | 1 |
