题目内容
已知等差数列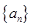 的首项为
的首项为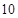 ,公差为
,公差为 ,数列
,数列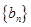 满足
满足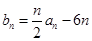 ,
,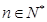 .
.
(1)求数列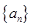 与
与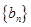 的通项公式;
的通项公式;
(2)记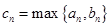 ,求数列
,求数列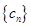 的前
的前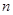 项和
项和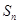 .
.
(注: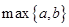 表示
表示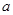 与
与 的最大值.)
的最大值.)
(1)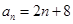 ,
,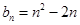 ;(2)
;(2)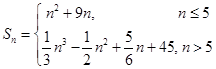 .
.
解析试题分析:(1)利用等差数列的通项公式求出数列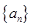 的通项公式,再将数列
的通项公式,再将数列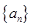 的通项公式代入
的通项公式代入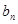 的表达式即可求出数列
的表达式即可求出数列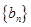 的通项公式;(2)利用作差法比较
的通项公式;(2)利用作差法比较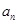 与
与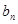 的大小,然后利用定义求出数列
的大小,然后利用定义求出数列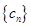 的通项公式(利用分段表达式进行表示),然后对
的通项公式(利用分段表达式进行表示),然后对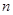 的取值分段求出
的取值分段求出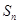 .
.
试题解析:(1)由于数列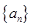 是以
是以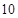 为首项,以
为首项,以 为公差的等差数列,
为公差的等差数列,
因此 ,
,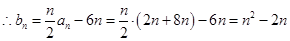 ;
;
(2)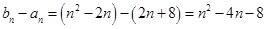 ,
,
令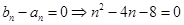 ,解得
,解得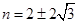 ,
,
因此当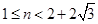 时,
时,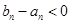 ,即
,即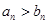 ,
,
因此当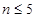 且
且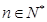 时,
时,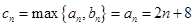 ,
,
当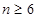 且
且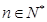 时,
时,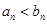 ,
,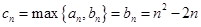 ,
,
当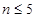 且
且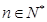
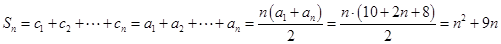 ,
,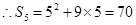 ,
,
当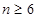 且
且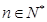 时,
时,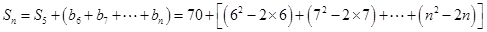
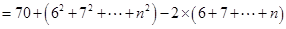
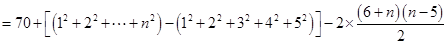
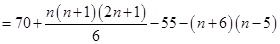
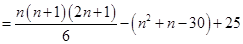
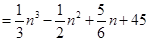 ,
,
所以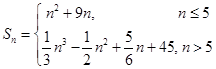 .
.
考点:1.等差数列的通项公式;2.利用作差法比较大小;3.分段求和

练习册系列答案
相关题目
 的公差为
的公差为 ,且
,且 .若设
.若设 是从
是从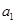 开始的前
开始的前 项数列的和,即
项数列的和,即 ,
, ,如此下去,其中数列
,如此下去,其中数列 是从第
是从第 开始到第
开始到第 )项为止的数列的和,即
)项为止的数列的和,即 .
. ,试找出一组满足条件的
,试找出一组满足条件的 ,使得:
,使得:  ;
; ,一定可通过适当的划分,使所得的数列
,一定可通过适当的划分,使所得的数列 中的各数都为平方数;
中的各数都为平方数; .试探索该数列中是否存在无穷整数数列
.试探索该数列中是否存在无穷整数数列 ,使得
,使得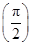 =0.
=0.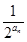 ),求数列{bn}的前n项和Sn.
),求数列{bn}的前n项和Sn.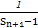 ,其前n项和为Tn,求证:Tn<
,其前n项和为Tn,求证:Tn< (n∈N*).
(n∈N*).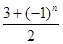 ,数列{an}满足an=d1+d2+d3+…+d2n,又知在数列{bn}中,b1=2,且对任意正整数m,n,
,数列{an}满足an=d1+d2+d3+…+d2n,又知在数列{bn}中,b1=2,且对任意正整数m,n, .
. 求a1+a2+a3+a4+…+a99+a100的值.
求a1+a2+a3+a4+…+a99+a100的值.