Question

函数y=2^x-2和y=

1

3

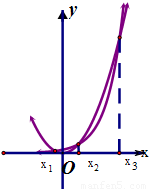
x²的图象如图所示，其中有且只有X=x₁，x₂，x₃时，两函数值相等，
且x₁＜0＜x₂＜x₃，0为坐标原点．现给出下列三个结论：
①当x∈（-∞，-1）时，2^x-2＜x²；
②x₂∈（1，2）；
③x₃∈（4，5）．其中正确结论的序号为______．

Answer 1

设函数f（x）=2^x-2-

1

3

x²，
∵f（-1）=

1

8

-

1

3

＜0，f（0）=

1

4

＞0
∴f（x）的一个零点在（-1，0）上，即-1＜x₁＜0，①正确；
∵f（1）=

1

2

-

1

3

＞0，f（2）=1-

4

3

＜0
∴1＜x₂＜2，②正确
同理，f（4）=4-

16

3

＜0，f（5）=8-

25

3

＜0，f（6）=16-

36

3

＞0
∴5＜x₃＜6，③错误
故答案为①②