题目内容
在数列{an} 中,a1=1,an+1=1-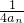 ,bn=
,bn=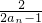 ,其中n∈N+,
,其中n∈N+,
(Ⅰ)求证:数列{bn} 是等差数列,并求数列{an} 的通项公式an;
(Ⅱ)设cn=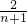 an,数列{CnCn+1} 的前n项和为Tn,是否存在正整整m,使得Tn<
an,数列{CnCn+1} 的前n项和为Tn,是否存在正整整m,使得Tn< 对于n∈N+恒成立,若存在,求出m的最大值,若不存在,说明理由.
对于n∈N+恒成立,若存在,求出m的最大值,若不存在,说明理由.
(1)证明:∵a1=1,an+1=1-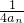 ,bn=
,bn=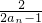 ,
,
∴bn+1-bn= =
= =
= -
-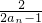 =2(n∈N*)
=2(n∈N*)
∴数列{bn}是等差数列,
∵a1=1,∴b1= =2,
=2,
∴bn=2+(n-1)×2=2n,
由bn=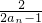 ,得2an-1=
,得2an-1= =
= ,(n∈N*)
,(n∈N*)
∴an= .
.
(2)∵cn=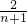 an=
an= =
= ,
,
∴CnCn+1= =
= ,
,
∴T=c1c2+c2c3+…+cncn+1
=(1- )+(
)+( )+(
)+(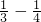 )+…+(
)+…+( )
)
=1- <1,
<1,
∵Tn=1- <
< 对于n∈N+恒成立,
对于n∈N+恒成立,
∴ ,∴m≤2,
,∴m≤2,
所以m的最大值为2.
分析:(1)要证数列{bn}是等差数列,只需证明bn+1-bn=2;
(2)由an= ,可得cn=
,可得cn=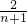 an=
an= =
= ,从而利用裂项法求前n项和为Tn,进而利用最值思想解决恒成立问题.
,从而利用裂项法求前n项和为Tn,进而利用最值思想解决恒成立问题.
点评:本题主要考查等差数列的定义及通项公式的求解,考查裂项法求和及恒成立问题的处理 方法,综合性强,难度大.
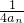 ,bn=
,bn=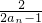 ,
,∴bn+1-bn=
 =
= =
= -
-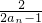 =2(n∈N*)
=2(n∈N*)∴数列{bn}是等差数列,
∵a1=1,∴b1=
 =2,
=2,∴bn=2+(n-1)×2=2n,
由bn=
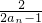 ,得2an-1=
,得2an-1= =
= ,(n∈N*)
,(n∈N*)∴an=
 .
.(2)∵cn=
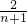 an=
an= =
= ,
,∴CnCn+1=
 =
= ,
,∴T=c1c2+c2c3+…+cncn+1
=(1-
 )+(
)+( )+(
)+(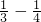 )+…+(
)+…+( )
)=1-
 <1,
<1,∵Tn=1-
 <
< 对于n∈N+恒成立,
对于n∈N+恒成立,∴
 ,∴m≤2,
,∴m≤2,所以m的最大值为2.
分析:(1)要证数列{bn}是等差数列,只需证明bn+1-bn=2;
(2)由an=
 ,可得cn=
,可得cn=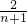 an=
an= =
= ,从而利用裂项法求前n项和为Tn,进而利用最值思想解决恒成立问题.
,从而利用裂项法求前n项和为Tn,进而利用最值思想解决恒成立问题.点评:本题主要考查等差数列的定义及通项公式的求解,考查裂项法求和及恒成立问题的处理 方法,综合性强,难度大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目