Question

一艘渔艇停泊在距央岸9 km处,今需派人送信给距渔艇 km处的海岸渔站,如果送信人步行每小时5 km,船速每小时4 km,问应在何处登岸再步行可以使抵达渔站的时间最省?

Answer 1

思路分析:如图1-4-3,设BC为海岸线,A为渔艇停泊处,设D为海岸线上一点,CD=x,将时间T表示成为关于x的形式,即可确定登岸的位置.

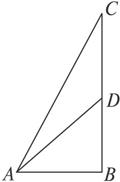
图1-4-3

解:∵AB=9,AC=,BC==15,

由A到C所需时间为T,则T=x+(0≤x≤15),

T′=.

令T′=0,解得x=3.

在x=3附近,T′由负到正,因此T在x=3处取得极小值.

又T(0)=,T(15)=,T(3)=,比较可知T(3)最小.

答:在距渔站3 km处登岸再步行可以使抵达渔站的时间最省.

    深化升华 在分析题意的基础上,建立函数的表达式时,一定要选择好自变量,同时准确确定自变量的取值范围.