题目内容
已知数列{an}的前n项和为Sn,且满足an= Sn+1(n∈N*);
Sn+1(n∈N*);
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=log2an,cn= ,且{cn}的前n项和为Tn,求使得
,且{cn}的前n项和为Tn,求使得 对n∈N*都成立的所有正整数k的值.
对n∈N*都成立的所有正整数k的值.
解:(1)an= Sn+1①
Sn+1①
an-1= Sn-1+1(n≥2)②
Sn-1+1(n≥2)②
①-②得:an=2an-1(n≥2),又易得a1=2∴an=2n(4分)
(2)bn=n, =
=
裂项相消可得 =
=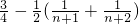 (8分)
(8分)
∵ (10分)
(10分)
∴欲 对n∈N*都成立,须
对n∈N*都成立,须 ,
,
又k正整数,∴k=5、6、7(12分)
分析:(1)由an= Sn+1,知an-1=
Sn+1,知an-1= Sn-1+1(n≥2),从而an=2an-1(n≥2),由此能够求出数列{an}的通项公式;
Sn-1+1(n≥2),从而an=2an-1(n≥2),由此能够求出数列{an}的通项公式;
(2)bn=n, =
= ,裂项相消得
,裂项相消得 =
=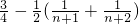 ,
, ,由此能求出使得
,由此能求出使得 对n∈N*都成立的所有正整数k的值.
对n∈N*都成立的所有正整数k的值.
点评:本题考查求解数列通项公式的方法和裂项求和法的应用,解题时要灵活运用不等式的性质求解参数的取值范围.
 Sn+1①
Sn+1①an-1=
 Sn-1+1(n≥2)②
Sn-1+1(n≥2)②①-②得:an=2an-1(n≥2),又易得a1=2∴an=2n(4分)
(2)bn=n,
 =
=
裂项相消可得
 =
=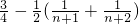 (8分)
(8分)∵
 (10分)
(10分)∴欲
 对n∈N*都成立,须
对n∈N*都成立,须 ,
,又k正整数,∴k=5、6、7(12分)
分析:(1)由an=
 Sn+1,知an-1=
Sn+1,知an-1= Sn-1+1(n≥2),从而an=2an-1(n≥2),由此能够求出数列{an}的通项公式;
Sn-1+1(n≥2),从而an=2an-1(n≥2),由此能够求出数列{an}的通项公式;(2)bn=n,
 =
= ,裂项相消得
,裂项相消得 =
=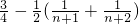 ,
, ,由此能求出使得
,由此能求出使得 对n∈N*都成立的所有正整数k的值.
对n∈N*都成立的所有正整数k的值.点评:本题考查求解数列通项公式的方法和裂项求和法的应用,解题时要灵活运用不等式的性质求解参数的取值范围.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |