题目内容
已知 f(x)为R上的可导函数,且f(x)<f'(x)和f(x)>0对于x∈R恒成立,则有
- A.f(2)<e2-f(0),f(2010)>e2010-f(0)
- B.f(2)>e2-f(0),f(2010)>e2010-f(0)
- C.f(2)<e2-f(0),f(2010)<e2010-f(0)
- D.f(2)<e2-f(0),f(2010)<e2010-f(0)
B
分析:先构造函数y=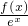 ,对该函数进行求导,化简变形可判定导函数的符号,再判断增减性,从而得到答案.
,对该函数进行求导,化简变形可判定导函数的符号,再判断增减性,从而得到答案.
解答:∵f(x)<f'(x) 从而 f'(x)-f(x)>0 从而 >0
>0
从而 >0 从而函数y=
>0 从而函数y=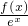 单调递增,故 x=2时函数的值大于x=0时函数的值,
单调递增,故 x=2时函数的值大于x=0时函数的值,
即 所以f(2)>e2f(0),f(2010)>e2010f(0).
所以f(2)>e2f(0),f(2010)>e2010f(0).
故选B.
点评:本题主要考查函数的单调性与其导函数的正负情况之间的关系,即导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.
分析:先构造函数y=
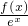 ,对该函数进行求导,化简变形可判定导函数的符号,再判断增减性,从而得到答案.
,对该函数进行求导,化简变形可判定导函数的符号,再判断增减性,从而得到答案.解答:∵f(x)<f'(x) 从而 f'(x)-f(x)>0 从而
 >0
>0从而
 >0 从而函数y=
>0 从而函数y=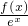 单调递增,故 x=2时函数的值大于x=0时函数的值,
单调递增,故 x=2时函数的值大于x=0时函数的值,即
 所以f(2)>e2f(0),f(2010)>e2010f(0).
所以f(2)>e2f(0),f(2010)>e2010f(0).故选B.
点评:本题主要考查函数的单调性与其导函数的正负情况之间的关系,即导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
已知f(x)为R上的减函数,则满足f(|
|)<f(1)的实数x的取值范围是( )
| 1 |
| x |
| A、(-1,1) |
| B、(0,1) |
| C、(-1,0)∪(0,1) |
| D、(-∞,-1)∪(1,+∞) |
已知 f(x)为R上的可导函数,且f(x)<f'(x)和f(x)>0对于x∈R恒成立,则有( )
| A、f(2)<e2-f(0),f(2010)>e2010-f(0) | B、f(2)>e2-f(0),f(2010)>e2010-f(0) | C、f(2)<e2-f(0),f(2010)<e2010-f(0) | D、f(2)<e2-f(0),f(2010)<e2010-f(0) |