题目内容
如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD是正三角形,且AD=DE=2AB,F是CD的中点.(1)求证:平面CBE⊥平面CDE;
(2)求二面角F-BE-C的大小.

(1)证明:∵DE⊥平面ACD,?
∴平面CDE⊥平面ACD.?
又∵AF⊥CD,?
∴AF⊥平面CDE.?
取CE的中点N,连结FN,BN,如图所示.?
∴FN ![]()
![]() DE=AB. ?
DE=AB. ?
∴四边形AFNB为平行四边形. ?
∴BN∥AF.
∴BN⊥平面CDE.?
∴平面CBE⊥平面CDE. .?
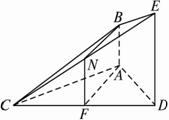
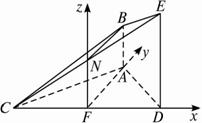
(2)解:建立如图所示的空间直角坐标系.?
设AB=1,则B(0,![]() ,1),F(0,0,0),C(-1,0,0),
,1),F(0,0,0),C(-1,0,0),![]() =(0,3,),
=(0,3,), ![]() =(1,0,2),
=(1,0,2),![]() =(1,3,1),
=(1,3,1), ![]() =(2,0,2). 7分?
=(2,0,2). 7分?
设平面FEB的法向量为n=(x,y,z),平面BCE的法向量为M=(p,q,r).?
则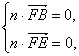 ?
?
即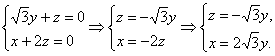 ?
?
令y=1,则n=(2![]() ,1,-
,1,-![]() ).?
).?
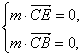 即
即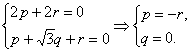 .?
.?
令r=1,则M=(-1,0,1). ?
∴cos〈m,n〉=![]() =
=![]() =-
=-![]() . ?
. ?
∴二面角F-BE-C的大小为π-arccos![]() . ?
. ?

 (2012•惠州模拟)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
(2012•惠州模拟)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点. (2012•枣庄一模)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
(2012•枣庄一模)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点. 如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD为等边三角形,AD=DE=2AB,F为CD的中点
如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD为等边三角形,AD=DE=2AB,F为CD的中点 如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.