Question

定理：三角形的外心O、重心G、垂心H依次在同一条直线（欧拉线）上，且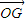=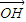，其中外心O是三条边的中垂线的交点，重心G是三条边的中线的交点，垂心H是三条高的交点．如图，在△ABC中，AB＞AC，AB＞BC，M是边BC的中点，AH⊥BC（N是垂足），O是外心，G是重心，H是垂心，OM=1，则根据定理可求得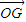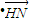的最大值是    ．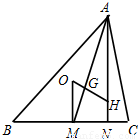

Answer 1

【答案】分析：以M为坐标原点，建立平面直角坐标系，根据已知逐一求出O，A，G，H，N及向量和的坐标，代入向量数量积的坐标公式，进而根据二次函数的图象和性质，求出的最大值
解答：解：以M为坐标原点，建立平面直角坐标系，如图所示：
∵OM=1，故O点的坐标为（0，1）
设A点坐标为（3x，3y），则N点坐标为（3x，0），
∵△ABC中，AB＞AC，故x＞0，y＞0
由G为△ABC的重心，故G点坐标为（x，y）
则=（x，y-1）
又∵=，
∴=（3x，3y-3），故H点的坐标是（3x，3y-2）
则=（0，2-3y）
则=（x，y-1）（0，2-3y）=-3y²+5y-2
故当y=时，取最大值
故答案为：
点评：本题考查的知识点是向量在几何中的应用，其中建立坐标系，将问题转化为求二次函数的最值问题是解答的关键．