题目内容
定义在R上的函数f(x)满足:f(1)=1,且对于任意的x∈R,都有f′(x)< ,则不等式f(log2x)>
,则不等式f(log2x)>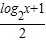 的解集为 .
的解集为 .
【答案】分析:设g(x)=f(x)- x,由f′(x)<
x,由f′(x)< ,得到g′(x)小于0,得到g(x)为减函数,将所求不等式变形后,利用g(x)为减函数求出x的范围,即为所求不等式的解集.
,得到g′(x)小于0,得到g(x)为减函数,将所求不等式变形后,利用g(x)为减函数求出x的范围,即为所求不等式的解集.
解答:解:设g(x)=f(x)- x,
x,
∵f′(x)< ,
,
∴g′(x)=f′(x)- <0,
<0,
∴g(x)为减函数,又f(1)=1,
∴f(log2x)>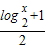 =
= log2x+
log2x+ ,
,
即g(log2x)=f(log2x)- log2x>
log2x> =g(1)=f(1)-
=g(1)=f(1)- =g(log22),
=g(log22),
∴log2x<log22,又y=log2x为底数是2的增函数,
∴0<x<2,
则不等式f(log2x)>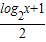 的解集为(0,2).
的解集为(0,2).
故答案为:(0,2)
点评:此题考查了其他不等式的解法,涉及的知识有:利用导数研究函数的增减性,对数函数的单调性及特殊点,以及对数的运算性质,是一道综合性较强的试题.
 x,由f′(x)<
x,由f′(x)< ,得到g′(x)小于0,得到g(x)为减函数,将所求不等式变形后,利用g(x)为减函数求出x的范围,即为所求不等式的解集.
,得到g′(x)小于0,得到g(x)为减函数,将所求不等式变形后,利用g(x)为减函数求出x的范围,即为所求不等式的解集.解答:解:设g(x)=f(x)-
 x,
x,∵f′(x)<
 ,
,∴g′(x)=f′(x)-
 <0,
<0,∴g(x)为减函数,又f(1)=1,
∴f(log2x)>
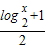 =
= log2x+
log2x+ ,
,即g(log2x)=f(log2x)-
 log2x>
log2x> =g(1)=f(1)-
=g(1)=f(1)- =g(log22),
=g(log22),∴log2x<log22,又y=log2x为底数是2的增函数,
∴0<x<2,
则不等式f(log2x)>
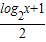 的解集为(0,2).
的解集为(0,2).故答案为:(0,2)
点评:此题考查了其他不等式的解法,涉及的知识有:利用导数研究函数的增减性,对数函数的单调性及特殊点,以及对数的运算性质,是一道综合性较强的试题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目