Question

以圆x²+y²-2x-2y-1=0内横坐标与纵坐标均为整数的点为顶点的三角形的个数为（　　）

A．76

B．78

C．81

D．84

Answer 1

分析：将圆化成标准方程，得圆心C（1，1），半径r=

3

，可得在圆内且横坐标与纵坐标均为整数的点有9个．然后利用组合数公式，采用间接法即可算出满足条件的三角形的个数．

解答：解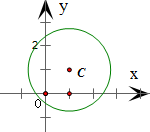：∵圆x²+y²-2x-2y-1=0化成标准形式，得
（x-1）²+（y-1）²=3
∴圆心C（1，1），半径r=

3

满足横坐标与纵坐标均为整数的点，且在圆内的点有
（0，0），（0，1），（0，2），（1，0），（1，1），（1，2），
（2，0），（2，1），（2，2）共9个点
9个点中任取3个，共有C93=84种取法，其中三点共线的情况共有8种
∴这9个点能构成三角形的个数为84-8=76个
故选：A

点评：本题给出圆方程，求圆内横坐标与纵坐标均为整数的点为顶点的三角形的个数．着重考查了圆的方程、点与圆的位置关系和排列组合计算公式等知识，属于中档题．