题目内容
(本小题满分12分)已知函数 的图象在点
的图象在点 处的切线方程为
处的切线方程为 .
.
(1)用 表示出
表示出 ;
;
(2)若 在
在 上恒成立,求
上恒成立,求 的取值范围;
的取值范围;
(3)证明: .
.
【答案】
【解析】(Ⅰ) ,则有
,则有 ,解得
,解得  ….3分
….3分
(Ⅱ)由(Ⅰ)知, ,
,
令 ,
,
则  ,
, ………….5分
………….5分
(i)当
 ,
,
若  ,则
,则 ,
,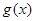 是减函数,所以
是减函数,所以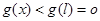
 ,故
,故 在
在 上恒不成立。
上恒不成立。
(ii) 时,
时, ………………………………….7分
………………………………….7分
若 ,故当
,故当 时,
时, 综上所述,
综上所述,
所求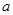 的取值范围为
的取值范围为
(Ⅲ)解法一:由(Ⅱ)知:当 时,有
时,有 。
。
令 ,有
,有
当 时,
时,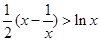 。…………………………8分
。…………………………8分
令 ,有
,有
即 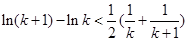 ,
,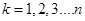 …………………….10分
…………………….10分
将上述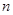 个不等式一次相加得
个不等式一次相加得

整理得: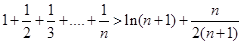 …………………….12分
…………………….12分
解法二:用数学归纳法证明
(1)当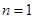 时,左边
时,左边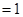 ,右边
,右边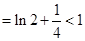 ,不等式成立…………….8分
,不等式成立…………….8分
(2)假设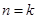 时, 不等式成立, 就是
时, 不等式成立, 就是

那么
 ………………………………….9分
………………………………….9分
由(Ⅱ)知:当 时,有
时,有
令 ,有
,有 …………………………10分
…………………………10分
令 ,得:
,得: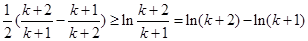

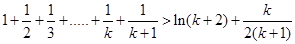 ………………………12分
………………………12分
就是说, 当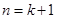 时,不等式也成立。
时,不等式也成立。
根据(1)和(2),可知不等式对任何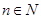 都成立。
都成立。

练习册系列答案
相关题目