题目内容
(本小题满分12分)
已知平面直角坐标系中, ,
, ,
, ,
, .
.
(Ⅰ)求 的最小正周期和对称中心;
的最小正周期和对称中心;
(Ⅱ)求 在区间
在区间 上的单调递增区间.
上的单调递增区间.
(Ⅰ)故最小正周期为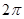 ,对称中心是
,对称中心是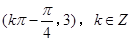 ;
;
(Ⅱ) 的递增区间为
的递增区间为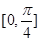 和
和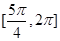 。
。
解析试题分析:(I)先根据向量的坐标的加法运算法则求出向量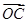 的坐标,从而求出
的坐标,从而求出
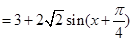
从而可得其周期为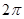 ,再利用正弦函数的对称中心
,再利用正弦函数的对称中心 ,可求出f(x)的对称中心.
,可求出f(x)的对称中心.
(II)由正弦函数的单调增区间可知当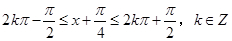 时
时 单增,解此不等式可求出f(x)的单调增区间,然后给k赋值,可得f(x)在
单增,解此不等式可求出f(x)的单调增区间,然后给k赋值,可得f(x)在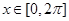 上的增区间.
上的增区间.
(Ⅰ)由题设知,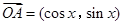 ,……………………1分
,……………………1分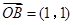 ,则
,则
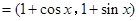 …………………2分
…………………2分

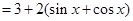 ……………………………………4分
……………………………………4分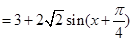 ………………………………………………5分
………………………………………………5分
故最小正周期为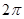 ………………………………………………6分
………………………………………………6分
对称中心横坐标满足 ,即
,即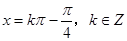
对称中心是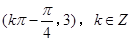 ………………………………………………8分
………………………………………………8分
(Ⅱ)当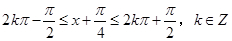 时
时 单增,……………9分
单增,……………9分
即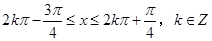 ……………………………………10分
……………………………………10分
又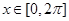 ,故
,故 的递增区间为
的递增区间为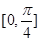 和
和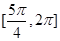 ………………………12分
………………………12分
考点:向量的坐标运算,正弦型函数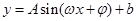 的周期,对称中心,以及单调区间.
的周期,对称中心,以及单调区间.
点评:掌握向量的坐标运算是解好本题的前题,理解并把握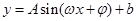 的周期,对称中心,对称轴,以及单调区间的求法是解题的关键.
的周期,对称中心,对称轴,以及单调区间的求法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 其中
其中 ,
,
 求
求 的值;(4分)
的值;(4分)  的图像的相邻两条对称轴之间的距离等于
的图像的相邻两条对称轴之间的距离等于 ,
, ,使得函数
,使得函数 为第三象限角,
为第三象限角,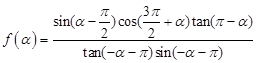 .
. ;
; ,求
,求

 =
= ,且
,且 . (1)求角C; (2)若
. (1)求角C; (2)若 ,试求
,试求 的值.
的值. ,(
,( )
) 的最小正周期和单调递增区间;
的最小正周期和单调递增区间; 时,求
时,求 是
是 的导函数.
的导函数. ,求
,求 的值.
的值.  (
( )的单调增区间。
)的单调增区间。  上的函数
上的函数 ,最大值与最小值的差为4,相邻两个最低点之间距离为
,最大值与最小值的差为4,相邻两个最低点之间距离为 ,函数
,函数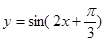 图象所有对称中心都在
图象所有对称中心都在 图象的对称轴上.
图象的对称轴上. ,求
,求 的值;
的值;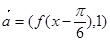 ,
, ,
, ,若
,若 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.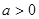 ,函数
,函数 ,
, 时,
时, ,求常数
,求常数 ,
, 的值.
的值.