题目内容
设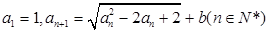
(1)若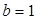 ,求
,求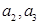 及数列
及数列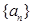 的通项公式;
的通项公式;
(2)若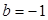 ,问:是否存在实数
,问:是否存在实数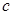 使得
使得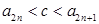 对所有
对所有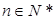 成立?证明你的结论.
成立?证明你的结论.
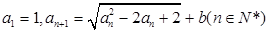
(1)若
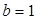 ,求
,求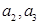 及数列
及数列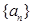 的通项公式;
的通项公式;(2)若
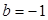 ,问:是否存在实数
,问:是否存在实数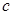 使得
使得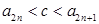 对所有
对所有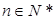 成立?证明你的结论.
成立?证明你的结论.(1)
 ;(2)存在,
;(2)存在,

 ;(2)存在,
;(2)存在,
试题分析:(1)由


所以数列
 是等差数列,可先求数列
是等差数列,可先求数列 再求数列
再求数列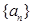 的通项公式;也可以先根据数列
的通项公式;也可以先根据数列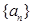 的前几项归纳出数列
的前几项归纳出数列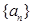 的通项公式,然后由数学归纳法证明.
的通项公式,然后由数学归纳法证明.(2)利用数列的递推公式
 构造函数
构造函数 ,
,由
 ,然后结合函数
,然后结合函数 的单调性,用数学归纳法证明
的单调性,用数学归纳法证明 即可.
即可.解:(1)解法一:

再由题设条件知

从而
 是首项为0公差为1的等差数列,
是首项为0公差为1的等差数列,故
 =
= ,即
,即
解法二:

可写为
 .因此猜想
.因此猜想 .
.下用数学归纳法证明上式:
当
 时结论显然成立.
时结论显然成立.假设
 时结论成立,即
时结论成立,即 .则
.则
这就是说,当
 时结论成立.
时结论成立.所以

(2)解法一:设
 ,则
,则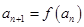 .
.令
 ,即
,即 ,解得
,解得 .
.下用数学归纳法证明加强命:

当
 时,
时, ,所以
,所以 ,结论成立.
,结论成立.假设
 时结论成立,即
时结论成立,即
易知
 在
在 上为减函数,从而
上为减函数,从而
即

再由
 在
在 上为减函数得
上为减函数得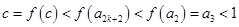 .
.故
 ,因此
,因此 ,这就是说,当
,这就是说,当 时结论成立.
时结论成立.综上,符合条件的
 存在,其中一个值为
存在,其中一个值为 .
.解法二:设
 ,则
,则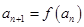
先证:
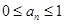
 ①
①当
 时,结论明显成立.
时,结论明显成立.假设
 时结论成立,即
时结论成立,即
易知
 在
在 上为减函数,从而
上为减函数,从而
即
 这就是说,当
这就是说,当 时结论成立,故①成立.
时结论成立,故①成立.再证:

 ②
②当
 时,
时, ,有
,有 ,即当
,即当 时结论②成立
时结论②成立假设
 时,结论成立,即
时,结论成立,即
由①及
 在
在 上为减函数,得
上为减函数,得

这就是说,当
 时②成立,所以②对一切
时②成立,所以②对一切 成立.
成立.由②得

即

因此

又由①、②及
 在
在 上为减函数得
上为减函数得
即

所以
 解得
解得 .
.综上,由②③④知存在
 使
使 对一切
对一切 成立.
成立.
练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
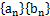 (
(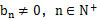 ),满足
),满足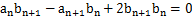 .
.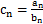 ,求数列
,求数列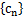 的通项公式;
的通项公式;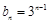 ,求数列
,求数列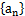 的前n项和
的前n项和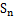
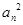 +n-4.
+n-4. 满足:
满足: ,且
,且 、
、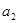 、
、 成等比数列.
成等比数列. 为数列
为数列 项和,是否存在正整数
项和,是否存在正整数 若存在,求
若存在,求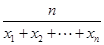 为n个正数x1,x2,…,xn的“平均倒数”,若正项数列{cn}的前n项的“平均倒数”为
为n个正数x1,x2,…,xn的“平均倒数”,若正项数列{cn}的前n项的“平均倒数”为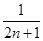 ,则数列{cn}的通项公式为cn=________.
,则数列{cn}的通项公式为cn=________. ,如果
,如果 为完全平方数,则称数列
为完全平方数,则称数列 ,且
,且 是
是 的一个排列;②数列
的一个排列;②数列 .
.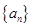 中,
中, ,那么数列
,那么数列 满足
满足 ,则
,则 ________.
________.