题目内容
已知O为坐标原点,
=(2cos2x,1),
=(1,
sin2x+a)(x∈R,a∈R,a是常数),若y=
•
(1)求y关于x的函数关系式f(x);
(2)若f(x)的最大值为2,求a的值;
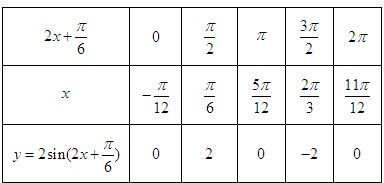
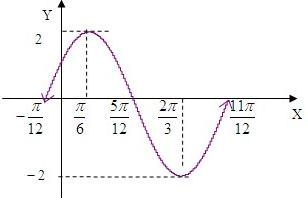
(3)利用(2)的结论,用“五点法”作出函数f(x)在长度为一个周期的闭区间上的简图,并指出其单调区间.
| OA |
| OB |
| 3 |
| OA |
| OB |
(1)求y关于x的函数关系式f(x);
(2)若f(x)的最大值为2,求a的值;
(3)利用(2)的结论,用“五点法”作出函数f(x)在长度为一个周期的闭区间上的简图,并指出其单调区间.
(1)∵
| OA |
| OB |
| 3 |
∴y=
| OA |
| OB |
| 3 |
(2)由(1)得y=2cos2x+
| 3 |
=1+cos2x+
| 3 |
=cos2x+
| 3 |
=2(
| 1 |
| 2 |
| ||
| 2 |
=2(sin
| π |
| 6 |
| π |
| 6 |
=2sin(2x+
| π |
| 6 |
当sin(2x+
| π |
| 6 |
又∵ymax=2
∴3+a=2
∴a=-1
(3)由(2)得,y=2sin(2x+
| π |
| 6 |
增区间是:[-
| π |
| 3 |
| π |
| 6 |
减区间是:[
| π |
| 6 |
| 2π |
| 3 |

练习册系列答案
相关题目