题目内容
已知y=f(x)定义在R上的单调函数,当x<0时,f(x)>1,且对任意的实数x、y∈R,有f(x+y)=f(x)•f(y).设数列{an}满足a1=f(0),且f(an+1)=| 1 |
| f(-2-an) |
(Ⅰ)求通项公式an的表达式;
(Ⅱ)令bn=(
| 1 |
| 2 |
| 1 |
| a1a2 |
| 1 |
| a2a3 |
| 1 |
| anan+1 |
| 4 |
| 3 |
分析:(Ⅰ)令y=0,x<0,得f(x)[1-f(0)]=0,由x<0,f(x)>1,知a1=f(0)=1,由递推关系知f(an+1-2-an)=f(0),由此能够推导出an.
(Ⅱ)由bn=(
)an=(
)2n-1,知Sn=b1+b2+…+bn=
+(
)3+…+(
)2n-1=
=
(1-
),Tn=
+
+…+
=
+
+…+
=
(1-
+
-
+…+
-
)=
(1-
),所以Sn-
Tn=
(1-
)-
(1-
)=
(
-
)=
•
,欲比较Sn与
Tn的大小,只需比较4n与2n+1的大小.
(Ⅱ)由bn=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||||
1-(
|
| 2 |
| 3 |
| 1 |
| 4n |
| 1 |
| a1a2 |
| 1 |
| a2a3 |
| 1 |
| anan+1 |
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 4 |
| 3 |
| 2 |
| 3 |
| 1 |
| 4n |
| 2 |
| 3 |
| 1 |
| 2n+1 |
| 2 |
| 3 |
| 1 |
| 2n+1 |
| 1 |
| 4n |
| 2 |
| 3 |
| 4n-(2n+1) |
| (2n+1)•4n |
| 4 |
| 3 |
解答:解:(Ⅰ)由题意,令y=0,x<0,得f(x)[1-f(0)]=0,
∵当x<0时,f(x)>1,∴a1=f(0)=1…(2分)
由递推关系知f(an+1)•f(-2-an)=1,即f(an+1-2-an)=f(0),
∵f(x)在R上单调,∴an+1-an=2,(n∈N*),…(4分)
又a1=1,∴an=2n-1.…(6分)
(Ⅱ)bn=(
)an=(
)2n-1,
∴Sn=b1+b2+…+bn=
+(
)3+…+(
)2n-1=
=
(1-
),Tn=
+
+…+
=
+
+…+
=
(1-
+
-
+…+
-
)=
(1-
),…(10分)Sn-
Tn=
(1-
)-
(1-
)=
(
-
)=
•
,
∴欲比较Sn与
Tn的大小,只需比较4n与2n+1的大小.…(11分)
∵4n=(1+3)n=Cn0+Cn1•3+…+Cnn•3n≥1+3n>2n+1,…(13分)
∴Sn>
Tn.…(14分)
∵当x<0时,f(x)>1,∴a1=f(0)=1…(2分)
由递推关系知f(an+1)•f(-2-an)=1,即f(an+1-2-an)=f(0),
∵f(x)在R上单调,∴an+1-an=2,(n∈N*),…(4分)
又a1=1,∴an=2n-1.…(6分)
(Ⅱ)bn=(
| 1 |
| 2 |
| 1 |
| 2 |
∴Sn=b1+b2+…+bn=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||||
1-(
|
| 2 |
| 3 |
| 1 |
| 4n |
| 1 |
| a1a2 |
| 1 |
| a2a3 |
| 1 |
| anan+1 |
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 4 |
| 3 |
| 2 |
| 3 |
| 1 |
| 4n |
| 2 |
| 3 |
| 1 |
| 2n+1 |
| 2 |
| 3 |
| 1 |
| 2n+1 |
| 1 |
| 4n |
| 2 |
| 3 |
| 4n-(2n+1) |
| (2n+1)•4n |
∴欲比较Sn与
| 4 |
| 3 |
∵4n=(1+3)n=Cn0+Cn1•3+…+Cnn•3n≥1+3n>2n+1,…(13分)
∴Sn>
| 4 |
| 3 |
点评:本题考查数列通项公式的求法和比较Sn与
Tn的大小.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
| 4 |
| 3 |

练习册系列答案
相关题目
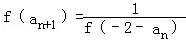 (n∈N*).
(n∈N*).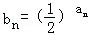 ,Sn=b1+b2+…+bn,
,Sn=b1+b2+…+bn,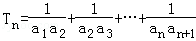 ,试比较Sn与
,试比较Sn与 的大小,并加以证明.
的大小,并加以证明. (n∈N*).
(n∈N*). ,Sn=b1+b2+…+bn,
,Sn=b1+b2+…+bn,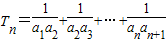 ,试比较Sn与
,试比较Sn与 的大小,并加以证明.
的大小,并加以证明.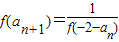 (n∈N*).
(n∈N*). ,Sn=b1+b2+…+bn,
,Sn=b1+b2+…+bn,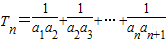 ,试比较Sn与
,试比较Sn与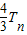 的大小,并加以证明.
的大小,并加以证明.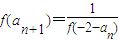 (n∈N*).
(n∈N*).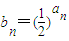 ,Sn=b1+b2+…+bn,
,Sn=b1+b2+…+bn,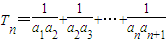 ,试比较Sn与
,试比较Sn与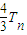 的大小,并加以证明.
的大小,并加以证明.