题目内容
已知动直线![]() 与圆
与圆![]()
(1) 求证:无论![]() 为何值,直线
为何值,直线![]() 与圆
与圆![]() 总相交.
总相交.
(2) ![]() 为何值时,直线
为何值时,直线![]() 被圆
被圆![]() 所截得的弦长最小?并求出该最小值.
所截得的弦长最小?并求出该最小值.
(1)证明 方法一 设圆心C(3,4)到动直线l的距离为d,则
d=![]() =
=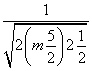 ≤
≤![]() .
.
∴当m=-![]() 时,dmax=
时,dmax=![]() <3(半径).
<3(半径).
故动直线l总与圆C相交.
方法二 直线l变形为m(x-y+1)+(3x-2y)=0.
令![]() 解得
解得![]()

如图所示,故动直线l恒过定点A(2,3).
而AC=![]() =
=![]() <3(半径).
<3(半径).
∴点A在圆内,故无论m取何值,直线l与圆C总相交.
(2)解 由平面几何知识知,弦心距越大,弦长越小,即当AC垂直直线l时,弦长最小.
∴最小值为2![]() =2
=2![]() .
.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
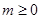 ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量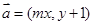 ,向量
,向量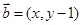 ,
,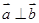 ,动点
,动点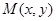 的轨迹为E.
的轨迹为E.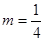 ,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且
,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且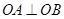 (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程;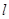 与圆C:
与圆C: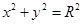 (1<R<2)相切于A1,且
(1<R<2)相切于A1,且