题目内容
设α、β为函数g(x)=2x2-mx-2的两个零点,m∈R且α<β,函数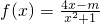 •
•
( I)求f(a)•g(x)的值;
(Ⅱ) 证明:函数f(x)在[α,β]上为增函数;
(III) 是否存在实数m,使得函数f(x)在[α,β]上的最大值与最小值之差达到最小.若存在,则求出实数m的值;否则,请说明理由.
解:( I)由题意可得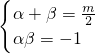 ,故 f(α)•f(β)=
,故 f(α)•f(β)=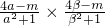 =
=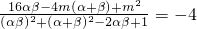 .(4分)
.(4分)
(Ⅱ)?x1,x2∈[α,β],x1<x2 ,可得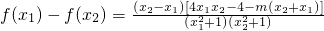 .
.
∵(x1-α)(x2-β)≤0,(x1-β)(x2-α)<0,两式相加可得 2x1x2-(α+β)(x1+x2)+2αβ<0.
∵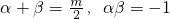 ,∴(x2-x1)[4x1x2-4-m(x2+x1)]<0,
,∴(x2-x1)[4x1x2-4-m(x2+x1)]<0,
∴f(x1)-f(x2)<0,∴函数f(x)在[α,β]上为增函数.(4分)
(III)函数f(x)在[α,β]上的最大值与最小值之差为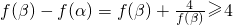 ,
,
当且仅当 f(β)=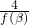 时,等号成立,此时,f(β)=2,即
时,等号成立,此时,f(β)=2,即 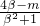 =2,2β2-mβ-2=0.
=2,2β2-mβ-2=0.
结合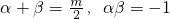 可得m=0.
可得m=0.
综上可得,存在实数m=0,满足条件.(5分)
分析:( I)由题意并根据一元二次方程根与系数的关系可得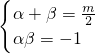 ,运算可得f(α)•f(β)=
,运算可得f(α)•f(β)=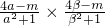 的值.
的值.
(Ⅱ)?x1,x2∈[α,β],x1<x2 ,依据条件判断f(x1)-f(x2)<0,从而得到函数f(x)在[α,β]上为增函数.
(III)函数f(x)在[α,β]上的最大值与最小值之差为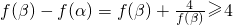 ,当且仅当 f(β)=
,当且仅当 f(β)=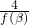 时,等号成立,此时,f(β)=2,即2β2-mβ-2=0,可得m=0.
时,等号成立,此时,f(β)=2,即2β2-mβ-2=0,可得m=0.
点评:本题主要考查函数的零点的定义,二次函数的性质,一元二次方程根与系数的关系,属于基础题.
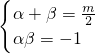 ,故 f(α)•f(β)=
,故 f(α)•f(β)=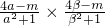 =
=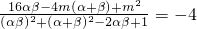 .(4分)
.(4分)(Ⅱ)?x1,x2∈[α,β],x1<x2 ,可得
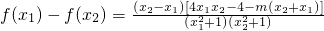 .
.∵(x1-α)(x2-β)≤0,(x1-β)(x2-α)<0,两式相加可得 2x1x2-(α+β)(x1+x2)+2αβ<0.
∵
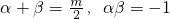 ,∴(x2-x1)[4x1x2-4-m(x2+x1)]<0,
,∴(x2-x1)[4x1x2-4-m(x2+x1)]<0,∴f(x1)-f(x2)<0,∴函数f(x)在[α,β]上为增函数.(4分)
(III)函数f(x)在[α,β]上的最大值与最小值之差为
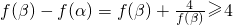 ,
,当且仅当 f(β)=
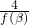 时,等号成立,此时,f(β)=2,即
时,等号成立,此时,f(β)=2,即 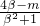 =2,2β2-mβ-2=0.
=2,2β2-mβ-2=0.结合
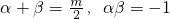 可得m=0.
可得m=0.综上可得,存在实数m=0,满足条件.(5分)
分析:( I)由题意并根据一元二次方程根与系数的关系可得
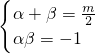 ,运算可得f(α)•f(β)=
,运算可得f(α)•f(β)=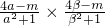 的值.
的值.(Ⅱ)?x1,x2∈[α,β],x1<x2 ,依据条件判断f(x1)-f(x2)<0,从而得到函数f(x)在[α,β]上为增函数.
(III)函数f(x)在[α,β]上的最大值与最小值之差为
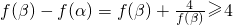 ,当且仅当 f(β)=
,当且仅当 f(β)=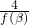 时,等号成立,此时,f(β)=2,即2β2-mβ-2=0,可得m=0.
时,等号成立,此时,f(β)=2,即2β2-mβ-2=0,可得m=0.点评:本题主要考查函数的零点的定义,二次函数的性质,一元二次方程根与系数的关系,属于基础题.

练习册系列答案
相关题目