Question

是否存在常数a、b、c使等式1·(n²-1²)+2(n²-2²)+…+n(n²-n²)=an⁴+bn²+c对一切正整数n成立?证明你的结论.

Answer 1

解：分别用n=1,2,3代入解方程组

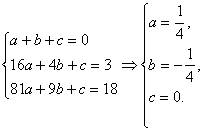
下面用数学归纳法证明.

(1)当n=1时,由上可知等式成立;

(2)假设当n=k时,等式成立;

则当n=k+1时,左边=1·［(k+1)²-1²］+2［(k+1)²-2²］+…+k［(k+1)²-k²］+(k+1)［(k+1)²-(k+1)²］=1(k²-1²)+2(k²-2²)+…+k(k²-k²)+1·(?2k+1)+2(2k+1)+…+k(2k+1)=k⁴+()k²+(2k+1)+2(2k+1)+…+k(2k+1)=(k+1)⁴(k+1)².

∴当n=k+1时,等式成立.

由(1)(2)得等式对一切的n∈N^*均成立.