题目内容
已知函数f(x)= 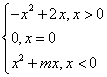 是奇函数
是奇函数
(1)求实数m的值.
(2)若函数f(x)在区间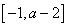 上单调递增,求实数a的取值范围.
上单调递增,求实数a的取值范围.
(1)m=2 ; (2)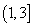 .
.
【解析】
试题分析:(1)因为函数是奇函数,故由f(-x)=-f(x),结合分段函数的解析,从而有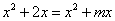 ,解得m=2;(2)根据(1)中所求
,解得m=2;(2)根据(1)中所求 ,利用函数的图像,可知函数
,利用函数的图像,可知函数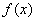 在
在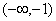 和
和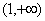 单调递减,在
单调递减,在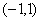 单调递增,又函数f(x)在区间
单调递增,又函数f(x)在区间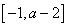 上单调递增,可知
上单调递增,可知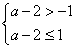 从而得出实数a的取值范围是
从而得出实数a的取值范围是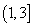 .
.
试题解析:(1)设x<0,则-x>0,  f(-x)=-
f(-x)=- 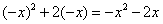 又f(x)为奇函数,………………3分
又f(x)为奇函数,………………3分
 f(-x)=-f(x),于是x<0时,f(x)=
f(-x)=-f(x),于是x<0时,f(x)= 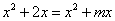 ,
,  m=2 …………6分
m=2 …………6分
(2)要使f(x)在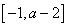 上单调递增,结合f(x)图像知
上单调递增,结合f(x)图像知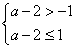 ………10分
………10分
 1<a
1<a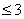 故实数a的取值范围是
故实数a的取值范围是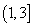 ………………12分
………………12分
考点:1.奇函数的性质;2.分段函数的奇偶性

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 +(y+1)2=0,则x=2且y=-1”的逆否命题为________
+(y+1)2=0,则x=2且y=-1”的逆否命题为________  且
且 是f(x)的导函数,若
是f(x)的导函数,若 ,,则
,,则 = .
= . 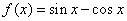 且
且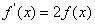 ,
,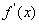 是f(x)的导函数,则
是f(x)的导函数,则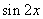 = ( )
= ( ) 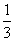 B.-
B.-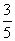 C.
C.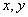 )坐标
)坐标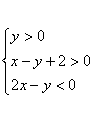 则
则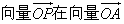 方向上的投影的取值范围是 .
方向上的投影的取值范围是 . 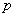 :
: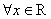 ,
,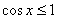 ,则
,则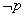 是( )
是( )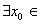 R,
R,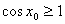 (B)
(B)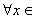 R,
R,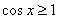
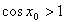 (D)
(D)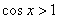
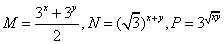 (
(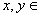 R
R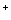 ,且
,且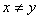 ), 则
), 则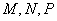 大小关系为( )
大小关系为( )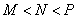 (B)
(B)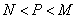 (C)
(C)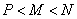 (D)
(D)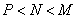
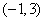 且与直线
且与直线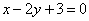 平行的直线方程为 ( )
平行的直线方程为 ( )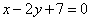 B.
B.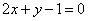 C.
C.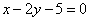 D.
D.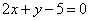
 B.
B.
 D.
D.