题目内容
在平面内与点 距离为1且与点
距离为1且与点 距离为2的直线共有 ( )
距离为2的直线共有 ( )
| A.1条 | B.2条 | C.3条 | D.4条 |
B
解析试题分析:以A点距离为1的所有直线是以A(1,2)为圆心,半径为1的圆的切线.同理到点 距离为2的直线是以
距离为2的直线是以 为圆心半径为2的圆的切线.同时满足即为两圆的公切线的条数.
为圆心半径为2的圆的切线.同时满足即为两圆的公切线的条数. 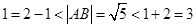 ,所以两圆相交,故有两条公切线.所以选B.
,所以两圆相交,故有两条公切线.所以选B.
考点:1.圆的切线的性质.2.两圆的位置关系的判定.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
过原点且倾斜角为 的直线被圆
的直线被圆 所截得的弦长为( )
所截得的弦长为( )
A. | B. | C. | D. |
直线 与圆C:
与圆C: 切于点
切于点 ,则a+b的值为( )
,则a+b的值为( )
| A.1 | B.-1 | C.3 | D.-3 |
已知实数 满足
满足 ,则
,则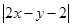 的最小值是( )
的最小值是( )
A. | B. | C. | D.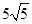 |
圆 的位置关系是( )
的位置关系是( )
| A.外离 | B.外切 | C.相交 | D.内含 |
若直线 被圆
被圆 截得的弦长为4,则
截得的弦长为4,则 的最小值是( )
的最小值是( )
A. | B. | C.3 | D. |
已知圆C与直线 及
及 都相切,圆心在直线
都相切,圆心在直线 上,则圆C的方程为( )
上,则圆C的方程为( )
A. | B. |
C. | D. |
已知圆心为 的圆,经过点
的圆,经过点 ,则该圆的标准方程是
,则该圆的标准方程是
A. |
B. |
C. |
D. |
 的左、右焦点分别为F1、F2,点P在右支上,且PF1与圆x2+y2=a2相切,切点为PF1的中点,F2到一条渐近线的距离为3,则
的左、右焦点分别为F1、F2,点P在右支上,且PF1与圆x2+y2=a2相切,切点为PF1的中点,F2到一条渐近线的距离为3,则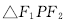 的面积为 ( )
的面积为 ( )