题目内容
已知椭圆的焦点为F1(-1,0)、F2(1,0),直线x=4是它的一条准线.(1)求椭圆的方程;
(2)设A1、A2分别是椭圆的左顶点和右顶点,P是椭圆上满足|PA1|-|PA2|=2的一点,求tan∠A1PA2的值;
(3)若过点(1,0)的直线与以原点为顶点、A2为焦点的抛物线相交于点M、N,求MN中点Q的轨迹方程.
解:(1)设椭圆方程为![]() +
+![]() =1(a>b>0).
=1(a>b>0).
由题设有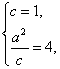
解得![]() ∴b2=3.所求椭圆方程为
∴b2=3.所求椭圆方程为![]() +
+![]() =1.
=1.
(2)由题设知,点P在以A1、A2为焦点,实轴长为2的双曲线的右支上.
由(1)知A1(-2,0),A2(2,0),
设双曲线方程为![]() -
-![]() =1(m>0,n>0).
=1(m>0,n>0).
则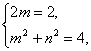 解得
解得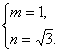
∴双曲线方程为x2-![]() =1.
=1.
由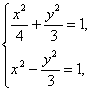
解得P点的坐标为(![]() ,
,![]() )或(
)或(![]() ,-
,-![]() ).当P点坐标为(
).当P点坐标为(![]() ,
,![]() )时,tan∠A1PA2=
)时,tan∠A1PA2=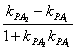 =-4
=-4![]() .
.
同理,当P点坐标为(![]() ,-
,-![]() )时,
)时,
tan∠A1PA2=-4![]() .
.
故tan∠A1PA2=-4![]() .
.
(3)由题设知,抛物线方程为y2=8x.
设M(x1,y1)、N(x2,y2),MN的中点Q(x,y),
当x1≠x2时,有
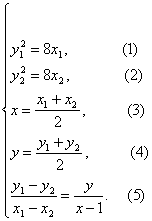
①-②,得![]() (y1+y2)=8,
(y1+y2)=8,
将④⑤代入上式,
有![]() ·2y=8,
·2y=8,
即y2=4(x-1)(x≠1).
当x1=x2时,MN的中点为(1,0),仍满足上式.
故所求点Q的轨迹方程为y2=4(x-1).

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目