题目内容
在平面直角坐标系xOy中,点An满足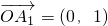 ,且
,且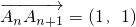 ;点Bn满足
;点Bn满足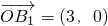 ,且
,且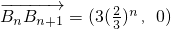 ,其中n∈N*.
,其中n∈N*.
(1)求 的坐标,并证明点An在直线y=x+1上;
的坐标,并证明点An在直线y=x+1上;
(2)记四边形AnBnBn+1An+1的面积为an,求an的表达式;
(3)对于(2)中的an,是否存在最小的正整数P,使得对任意n∈N*都有an<P成立?若存在,求P的值;若不存在,请说明理由.
解:(1)由已知条件得,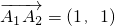 ,
,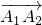 =
=
 ,∴
,∴ ,
,
∵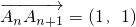 ,∴
,∴
设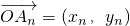 ,则xn+1-xn=1,yn+1-yn=1
,则xn+1-xn=1,yn+1-yn=1
∴xn=0+(n-1)•1=n-1;yn=1+(n-1)•1=n.
即An=(n-1,n)满足方程y=x+1,∴点An在直线y=x+1上.
(2)由(1)得An(n-1,n), ,
,
设Bn(un,vn),则u1=3,v1=0,vn+1-vn=0,∴vn=0,
 ,逐差累和得,
,逐差累和得,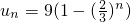 ,
,
∴ .
.
设直线y=x+1与x轴的交点P(-1,0),则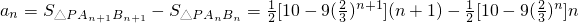 an=
an=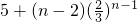 ,n∈N*.
,n∈N*.
(3)由(2)an=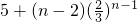 ,n∈N*
,n∈N*
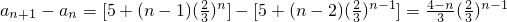 ,
,
于是,a1<a2<a3<a4=a5,a5>a6>a7>…
数列{an}中项的最大值为 ,则
,则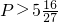 ,即最小的正整数p的值为6,
,即最小的正整数p的值为6,
所以,存在最小的自然数p=6,对一切n∈N*都有an<p成立.
分析:(1)利用向量的运算法则、等差数列的定义及通项公式即可证明;
(2)利用向量的运算法则和逐差累和即可求得点Bn的坐标,及 -
- 即可求出.
即可求出.
(3)利用(2)的结论及作差法,求出an+1-an,进而即可判断出答案.
点评:熟练掌握向量的运算法则、等差数列的定义及通项公式、逐差累和、及利用 -
- 求面积和作差法比较数的大小是解题的关键.
求面积和作差法比较数的大小是解题的关键.
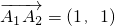 ,
,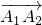 =
=
 ,∴
,∴ ,
,∵
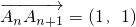 ,∴
,∴
设
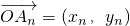 ,则xn+1-xn=1,yn+1-yn=1
,则xn+1-xn=1,yn+1-yn=1∴xn=0+(n-1)•1=n-1;yn=1+(n-1)•1=n.
即An=(n-1,n)满足方程y=x+1,∴点An在直线y=x+1上.
(2)由(1)得An(n-1,n),
 ,
,设Bn(un,vn),则u1=3,v1=0,vn+1-vn=0,∴vn=0,
 ,逐差累和得,
,逐差累和得,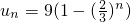 ,
,∴
 .
.设直线y=x+1与x轴的交点P(-1,0),则
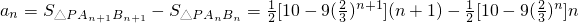 an=
an=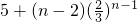 ,n∈N*.
,n∈N*.(3)由(2)an=
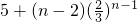 ,n∈N*
,n∈N*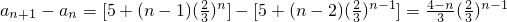 ,
,于是,a1<a2<a3<a4=a5,a5>a6>a7>…
数列{an}中项的最大值为
 ,则
,则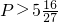 ,即最小的正整数p的值为6,
,即最小的正整数p的值为6,所以,存在最小的自然数p=6,对一切n∈N*都有an<p成立.
分析:(1)利用向量的运算法则、等差数列的定义及通项公式即可证明;
(2)利用向量的运算法则和逐差累和即可求得点Bn的坐标,及
 -
- 即可求出.
即可求出.(3)利用(2)的结论及作差法,求出an+1-an,进而即可判断出答案.
点评:熟练掌握向量的运算法则、等差数列的定义及通项公式、逐差累和、及利用
 -
- 求面积和作差法比较数的大小是解题的关键.
求面积和作差法比较数的大小是解题的关键. 
练习册系列答案
相关题目
 (2013•上海)在平面直角坐标系xOy中,点A在y轴正半轴上,点Pn在x轴上,其横坐标为xn,且{xn} 是首项为1、公比为2的等比数列,记∠PnAPn+1=θn,n∈N*.
(2013•上海)在平面直角坐标系xOy中,点A在y轴正半轴上,点Pn在x轴上,其横坐标为xn,且{xn} 是首项为1、公比为2的等比数列,记∠PnAPn+1=θn,n∈N*. 如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=x-3.设圆C的半径为1,圆心在l上.
如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=x-3.设圆C的半径为1,圆心在l上.