题目内容
已知函数f(x)=a|x|+ (a>0,a≠1)。
(a>0,a≠1)。
(1)若a>1,且关于x的方程f(x)=m有两个不同的正数解,求实数m的取值范围;
(2)设函数g(x)=f(-x),x∈[-2,+∞),g(x)满足如下性质:若存在最大(小)值,则最大(小)值与a无关,试求a的取值范围。
 (a>0,a≠1)。
(a>0,a≠1)。(1)若a>1,且关于x的方程f(x)=m有两个不同的正数解,求实数m的取值范围;
(2)设函数g(x)=f(-x),x∈[-2,+∞),g(x)满足如下性质:若存在最大(小)值,则最大(小)值与a无关,试求a的取值范围。
解:(1)令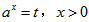 ,
,
因为a>1,所以t>1,
所以关于x的方程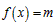 有两个不同的正数解等价于关于t的方程
有两个不同的正数解等价于关于t的方程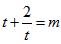 有相异的且均大于1的两根,即关于t的方程
有相异的且均大于1的两根,即关于t的方程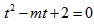 有相异的且均大于1的两根,
有相异的且均大于1的两根,
所以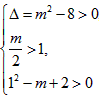 ,
,
解得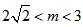 ,故实数m的取值范围为区间
,故实数m的取值范围为区间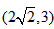 ;
;
(2)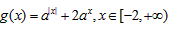
①当a>1时,
a)x≥0时,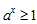 ,
,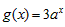 ,
,
所以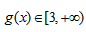 ,
,
b)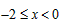 时,
时,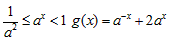 ,
,
所以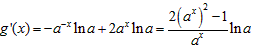 ,
,
ⅰ当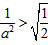 即
即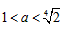 时,对
时,对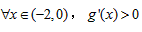 ,
,
所以g(x)在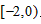 上递增,
上递增,
所以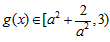 ,
,
综合a) b)g(x)有最小值为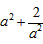 与a有关,不符合,
与a有关,不符合,
ⅱ当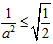 即
即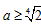 时,由
时,由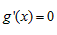 得
得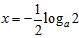 ,
,
且当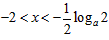 时,
时,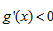 ,
,
当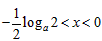 时,
时,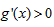 ,
,
所以g(x)在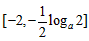 上递减,在
上递减,在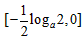 上递增,
上递增,
所以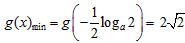 ,
,
综合a) b)g(x)有最小值为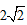 与a无关,符合要求,
与a无关,符合要求,
②当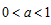 时,
时,
a)x≥0时,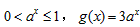 ,
,
所以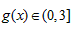
b)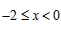 时,
时,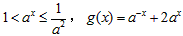 ,
,
所以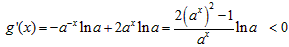 ,g(x)在
,g(x)在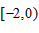 上递减,
上递减,
所以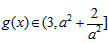 ,
,
综合a) b)g(x)有最大值为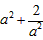 与a有关,不符合,
与a有关,不符合,
综上所述,实数a的取值范围是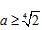 。
。

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目