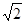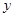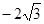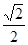题目内容
若存在过点 的直线与曲线
的直线与曲线 和
和 都相切,则
都相切,则

【答案】
 或
或
【解析】解:由y=x3⇒y'=3x2,设曲线y=x3上任意一点(x0,x03)处的切线方程为y- x03=3x02(x-x0),(1,0)代入方程得x0=0或x0=3 /2①当x0=0时,切线方程为y=0,则ax2+15 /4 x-9=0,△=(15/ 4 )2-4a×(-9)=0⇒a=-25/ 64
②当x0=3 2 时,切线方程为y=27/ 4 x-27/ 4 ,由 y=ax2+15 /4 x-9 y=27 /4 x-27/ 4 ⇒ax2-3x-9 /4 =0,△=32-4a(-9/ 4 )=0⇒a=-1∴a=-25/ 64 或a=-1.
故答案为:-25 /64 或-1

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
.(本小题满分14分)
已知椭圆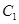 、抛物线
、抛物线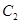 的焦点均在
的焦点均在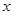 轴上,
轴上,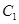 的中心和
的中心和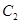 的顶点均为原点
的顶点均为原点 ,从每条曲
,从每条曲
线上取两个点,将其坐标记录于下表中:
|
|
3 |
|
4 |
|
|
|
|
0 |
|
|
(Ⅰ)求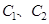 的标准方程;
的标准方程;
(Ⅱ)请问是否存在直线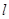 满足条件:①过
满足条件:①过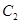 的焦点
的焦点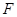 ;②与
;②与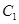 交不同两点
交不同两点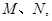 且满
且满
足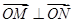 ?若存在,求出直线
?若存在,求出直线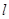 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
 2
2