题目内容
已知命题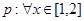 ,
,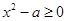 ,命题
,命题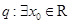 ,使得
,使得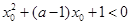 .若“
.若“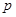 或
或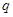 为真”,“
为真”,“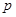 且
且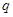 为假”,求实数
为假”,求实数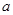 的取值范围.
的取值范围.
【答案】
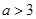 或
或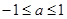 .
.
【解析】
试题分析:有条件求出命题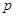 、
、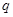 为真的
为真的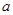 的取值范围,再由
的取值范围,再由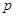 或
或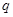 为真,
为真,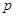 且
且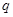 为假,
为假,
则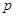 与
与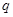 一真一假,分两种情况求出结论.
一真一假,分两种情况求出结论.
试题解析:由条件知,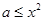 对
对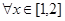 成立,∴
成立,∴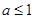 ;
;
∵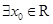 ,使得
,使得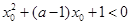 成立.
成立.
∴不等式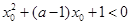 有解,∴
有解,∴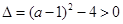 ,解得
,解得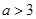 或
或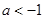 ;(6分)
;(6分)
∵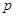 或
或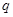 为真,
为真,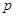 且
且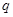 为假,
为假,
∴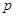 与
与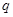 一真一假.
一真一假.
①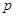 真
真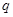 假时,
假时,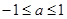 ;
;
②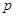 假
假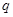 真时,
真时,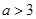 .
.
∴实数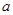 的取值范围是
的取值范围是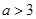 或
或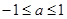 .
(12分)
.
(12分)
考点:复合命题的真假,函数的值域、函数的零点和函数的性质及应用.

练习册系列答案
相关题目
已知命题p:?x∈R,使sinx=
;命题q:?x∈R,都有x2+x+1>0.下列结论中正确的( )
| ||
| 2 |
| A、命题“p∧q”是真命题 |
| B、命题“p∧非q”是真命题 |
| C、命题“非p∧q”是真命题 |
| D、命题“非p∧q”是假命题 |
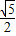 ;命题q:?x∈R,都有x2+x+1>0.下列结论中正确的( )
;命题q:?x∈R,都有x2+x+1>0.下列结论中正确的( ) ;命题q:?x∈R,都有x2+x+1>0.下列结论中正确的( )
;命题q:?x∈R,都有x2+x+1>0.下列结论中正确的( ) ;命题q:?x∈R,都有x2+x+1>0.下列结论中正确的( )
;命题q:?x∈R,都有x2+x+1>0.下列结论中正确的( ) ;命题q:?x∈R,都有x2+x+1>0.下列结论中正确的( )
;命题q:?x∈R,都有x2+x+1>0.下列结论中正确的( )