题目内容
（理）已知等差数列{an}的前n项和为Sn，且S10=
(1+2x)dx，S20=17，则S30为（ ）
| ∫ | 3 0 |
分析：根据等差数列前n项和的性质，写出一个新的等差数列，利用定积分求出前10项的和，根据性质列出关系式，得到结果．
解答：解：在等差数列中，s10，s20-s10，s30-s20成等差数列
∵S10=
(1+2x)dx=x+x2|
=3+9=12，
S20=17，
∴2（17-12）=12+s30-17
∴s30=15
故选A．
∵S10=
| ∫ | 3 0 |
| 3 |
| 0 |
S20=17，
∴2（17-12）=12+s30-17
∴s30=15
故选A．
点评：本题考查等差数列的性质和定积分，解题的关键是解出准确的定积分结果，这样才不会导致后面出错．
练习册系列答案
备战中考寒假系列答案
相关题目
，前n项和为Sn，且S4+a2=2S3；等比数列{bn}满足b1=a2，b2=a4
，求数列{cn}的前n项的和Tn
的最大值．
的公差是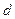
，
是该数列的前
项和.
表示
，其中
、
，求
项的和分别为
，试将问题（1）推广，探究相应的结论. 若能证明，则给出你的证明并求解以下给出的问题；若无法证明，则请利用你的研究结论和另一种方法计算以下给出的问题，从而对你猜想的可靠性作出自己的评价.问题：“已知等差数列
项和
，前
项和
，求数列
.”