题目内容
在F（x）中，已知内角A、B、C所对的边分别为a、b、c，向量
，
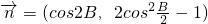，且
（I）求锐角B的大小；
（II）如果b=2，求F（x）的面积S△ABC的最大值．
解：（I）
由向量平行的坐标表示可得，由向量平行的坐标表示可得，
即2sinBcosB+
cos2B=0
∴sin2B+cos2B=0
∴
∵0＜B＜
∴B=
（II）∵b=2，B=60°
由余弦定理可得，4=b2=a2+c2-2ac×
=a2+c2-ac≥ac
∴ac≤4
∴S△ABC=
三角形的面积最大值为
分析：（I）由向量平行的坐标表示可得，，整理可得
结合已经知道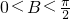
可求B
（II）；利用余弦定理可得4=a2+c2-ac，利用基本不等式可得ac≤4，代入面积公式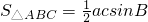
可求
点评：本题主要考查了向量平行的坐标表示，辅助角公式，由三角函数值班求角，余弦定理及基本不等式，三角形的面积公式等知识的综合运用．
由向量平行的坐标表示可得，由向量平行的坐标表示可得，
即2sinBcosB+
cos2B=0∴sin2B+
cos2B=0∴
∵0＜B＜
∴B=
（II）∵b=2，B=60°
由余弦定理可得，4=b2=a2+c2-2ac×
=a2+c2-ac≥ac∴ac≤4
∴S△ABC=
三角形的面积最大值为
分析：（I）由向量平行的坐标表示可得，
，整理可得结合已经知道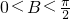可求B（II）；利用余弦定理可得4=a2+c2-ac，利用基本不等式可得ac≤4，代入面积公式
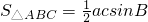可求点评：本题主要考查了向量平行的坐标表示，辅助角公式，由三角函数值班求角，余弦定理及基本不等式，三角形的面积公式等知识的综合运用．
练习册系列答案
相关题目
x-y+3+8
和圆C1：x2+y2+8x+F=0．若直线l被圆C1截得的弦长为2
．
x-y+3+8
和圆C1：x2+y2+8x+F=0．若直线l被圆C1截得的弦长为2
．
x-y+3+8
和圆C1：x2+y2+8x+F=0．若直线l被圆C1截得的弦长为2
．