题目内容
已知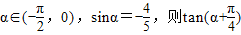 等于( )
等于( )A.-7
B.-

C.

D.7
【答案】分析:依题意,可求得tanα的值,利用两角和的正切公式即可求得tan(α+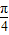 )的值.
)的值.
解答:解:∵α∈(-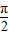 ,0),sinα=-
,0),sinα=- ,
,
∴cosα= ,
,
∴tanα=- .
.
∴tan(α+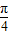 )=
)=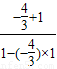 =-
=- .
.
故选B.
点评:本题考查两角和与差的正切函数,考查同角三角函数间的基本关系,求得tanα的值是关键,属于中档题.
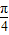 )的值.
)的值.解答:解:∵α∈(-
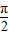 ,0),sinα=-
,0),sinα=- ,
,∴cosα=
 ,
,∴tanα=-
 .
.∴tan(α+
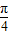 )=
)=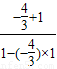 =-
=- .
.故选B.
点评:本题考查两角和与差的正切函数,考查同角三角函数间的基本关系,求得tanα的值是关键,属于中档题.

练习册系列答案
相关题目
 等于( )
等于( ) 等于( )
等于( ) 等于 ( )
等于 ( )
 等于 ( )
等于 ( ) 等于( )
等于( )